题目内容
从直线x-y+3=0上的点向圆(x+2)2+(y+2)2=1引切线,则切线长的最小值是
.
| ||
| 2 |
| ||
| 2 |
分析:先将切线长最小问题转化为圆心到直线距离最小问题,再利用点到直线的距离公式计算圆心到直线的最小距离,最后在直角三角形中由勾股定理计算切线长的最小值
解答:解: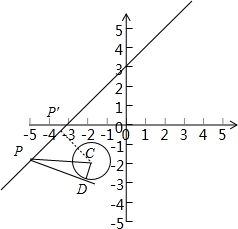 如图设从直线x-y+3=0上的点P向圆C:(x+2)2+(y+2)2=1引切线PD,切点为D,
如图设从直线x-y+3=0上的点P向圆C:(x+2)2+(y+2)2=1引切线PD,切点为D,
则CD|=1,在Rt△PDC中,要使切线长PD最小,只需圆心C到直线上点P的距离最小,
∵点C(-2,-2)到直线x-y+3=0的距离CP′最小为
=
∴切线长PD的最小值为
=
=
故答案为
 如图设从直线x-y+3=0上的点P向圆C:(x+2)2+(y+2)2=1引切线PD,切点为D,
如图设从直线x-y+3=0上的点P向圆C:(x+2)2+(y+2)2=1引切线PD,切点为D,则CD|=1,在Rt△PDC中,要使切线长PD最小,只需圆心C到直线上点P的距离最小,
∵点C(-2,-2)到直线x-y+3=0的距离CP′最小为
| |-2+2+3| | ||
|
3
| ||
| 2 |
∴切线长PD的最小值为
| P′C2-CD2 |
|
| ||
| 2 |
故答案为
| ||
| 2 |
点评:本题考察了直线与圆的位置关系,圆的标准方程,点到直线的距离公式和转化化归的思想方法,解题时特别注意几何条件在解题中的重要应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
从直线x-y+3=0上的点向圆(x+2)2+(y+2)2=1引切线,则切线长的最小值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
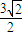
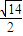
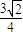
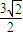 -1
-1