题目内容
从直线x-y+3=0上的点向圆(x+2)2+(y+2)2=1引切线,则切线长的最小值是( )A.
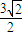
B.
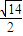
C.
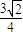
D.
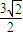 -1
-1
【答案】分析:根据圆的方程找出圆心坐标与半径,过圆心A作AP垂直于已知直线,垂足为P,此时过P作圆的切线,切线长最短,利用点到直线的距离公式求出|AP|的长,根据勾股定理求出|PQ|的长即为满足条件的切线长的最小值.
解答: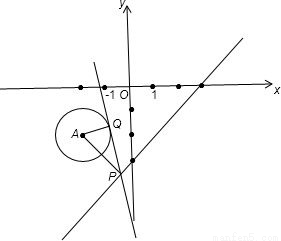 解:圆(x+2)2+(y+2)2=1的圆心A(-2,-2),
解:圆(x+2)2+(y+2)2=1的圆心A(-2,-2),
直线x-y+3=0上任一点P,过引圆的切线PQ(Q为切点),
则|PQ|=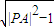 ,当且仅当|PA|最小时|PQ|最小,
,当且仅当|PA|最小时|PQ|最小,
易见|PA|的最小值即A到直线x-y+3=0的距离d,
d=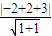 =
= ,
,
此时|PQ|=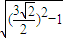 =
=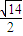 ,
,
故选B.
点评:此题要求学生掌握直线与圆的位置关系,灵活运用点到直线的距离公式及勾股定理化简求值,是一道中档题.
解答:
 解:圆(x+2)2+(y+2)2=1的圆心A(-2,-2),
解:圆(x+2)2+(y+2)2=1的圆心A(-2,-2),直线x-y+3=0上任一点P,过引圆的切线PQ(Q为切点),
则|PQ|=
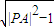 ,当且仅当|PA|最小时|PQ|最小,
,当且仅当|PA|最小时|PQ|最小,易见|PA|的最小值即A到直线x-y+3=0的距离d,
d=
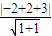 =
= ,
,此时|PQ|=
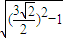 =
=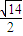 ,
,故选B.
点评:此题要求学生掌握直线与圆的位置关系,灵活运用点到直线的距离公式及勾股定理化简求值,是一道中档题.

练习册系列答案
相关题目
从直线x-y+3=0上的点向圆(x+2)2+(y+2)2=1引切线,则切线长的最小值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|