题目内容
20．一名篮球运动员在比赛时罚球命中率为80%，则他在3次罚球中罚失1次的概率是（ ）| A． | 0.384 | B． | 0.096 | C． | 0.616 | D． | 0.904 |
分析 设随机变量X表示“3次罚球，中的次数”，则X～B（3，0.8）．即可求出．
解答 解：设随机变量X表示“3次罚球，中的次数”，则X～B（3，0.8）．
则他在3次罚球中罚失1次的概率是P（X=2）=${C}_{3}^{2}$×0.82×（1-0.8）=0.384．
故选：A．
点评 本题主要考查了二项分布与n次独立重复试验的模型．熟练掌握二项分布是解题的关键．
练习册系列答案
相关题目
10．设y=f（t）是某港口水的深度关于时间t（时）的函数，其中0＜t≤24，下表是该港口某一天从0至24时记录的时间t与水深y的关系．
经长期观察，函数y=f（t）的图象可以近似地看成函数y=k+Asin（ωt-φ）的图象．根据上述数据，函数y=f（t）的解析式为（ ）
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
| A． | y=12+3sin$\frac{πt}{6}$，t∈[0，24] | B． | y=12+3sin（$\frac{πt}{6}$+π），t∈[0，24] | ||
| C． | y=12+3sin$\frac{πt}{12}$，t∈[0，24] | D． | y=12+3sin（$\frac{πt}{12}$+$\frac{π}{2}$），t∈[0，24] |
11．已知sin（$\frac{π}{2}$-α）=$\frac{5}{13}$，且α是第四象限的角，则tan（2π-α）=（ ）
| A． | -$\frac{12}{5}$ | B． | $\frac{12}{5}$ | C． | ±$\frac{12}{5}$ | D． | ±$\frac{5}{12}$ |
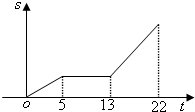某同学来学校上学，时间t（分钟）与路程s（米）的函数关系如图所示，现有如下几种说法：