Question

20．已知f（x）=|x|（x-2），如果关于x的方程f²（x）+2af（x）+1=0有三个不等实根，则a取值范围是（1，+∞）．

Answer 1

分析 作出y=f（x）的图象，由图象可得-1＜t＜0时，有3个交点，t²+2at+1=0有解，即有-2a=t+$\frac{1}{t}$，求得右边的范围，即可得到a的范围．

解答 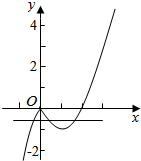解：f（x）=|x|（x-2）=$\left\{\begin{array}{l}{{x}^{2}-2x，x≥0}\\{2x-{x}^{2}，x＜0}\end{array}\right.$，作出y=f（x）的图象，
令t=f（x），
由图象可得-1＜t＜0时，有3个交点，
则t²+2at+1=0有解，
即有-2a=t+$\frac{1}{t}$，
由t+$\frac{1}{t}$＜-2，可得-2a＜-2，
解得a＞1．
故答案为：（1，+∞）．

点评 本题考查函数和方程的关系，考查二次方程有解的条件，注意运用数形结合的思想方法，属于中档题．