题目内容
已知二次函数 ,及函数
,及函数 。
。
关于 的不等式
的不等式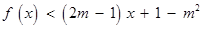 的解集为
的解集为 ,其中
,其中 为正常数。
为正常数。
(1)求 的值;
的值;
(2) R
R 如何取值时,函数
如何取值时,函数

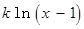 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若 ,且
,且
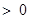 ,求证:
,求证:
 。
。
(1) (2)
(2) ,
, 
(3)可用数学归纳法证明
解析试题分析:(1)解:∵关于 的不等式
的不等式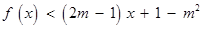 的解集为
的解集为 ,
,
即不等式 的解集为
的解集为 ,
,
∴
 .
.
∴
 .
.
∴ .
.
∴ .
.
(2)解法1:由(1)得
 .
.
∴
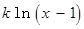

 的定义域为
的定义域为 .
.
∴

 .
.
方程 (*)的判别式
(*)的判别式 .
.
当 时,
时, 对
对 恒成立,方程(*)的两个实根为
恒成立,方程(*)的两个实根为

则 时,
时, ;
; 时,
时, .
.
∴函数 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
∴对任意实数k,函数 都有极小值点
都有极小值点 .
.
解法2:由(1)得
 .
.
∴
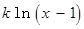

 的定义域为
的定义域为 .
.
∴

 .
.
若函数
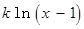 存在极值点等价于函数
存在极值点等价于函数 有两个不等的零点,且至少有一个零点在
有两个不等的零点,且至少有一个零点在 上.
上.
令

 ,
,
得
 , (*)
, (*)
则 ,(**)
,(**)
方程(*)的两个实根为 ,
,  .
.
设
 ,
,
①若 ,则
,则

练习册系列答案
相关题目
 的最大允许值是多少?
的最大允许值是多少?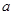 米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少? 是偶函数,
是偶函数, ,
, 的值;(2)当
的值;(2)当 时,求
时,求 的解集;
的解集; 的图象总在
的图象总在 的图象上方,求实数
的图象上方,求实数 的取值范围.
的取值范围. .
.  ;
; 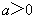 ,求证:
,求证: ≤
≤ .
. ,
, 是定义域为R上的奇函数.
是定义域为R上的奇函数. 的值,并证明当
的值,并证明当 时,函数
时,函数 ,函数
,函数 ,
, ,求
,求 的值域;
的值域;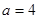 ,试问是否存在正整数
,试问是否存在正整数 ,使得
,使得 对
对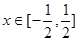 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数 (元)与月处理量
(元)与月处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元. 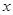 万件,需另投入流动成本为
万件,需另投入流动成本为 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,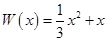 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,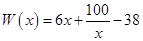 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.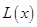 (万元)关于年产量
(万元)关于年产量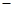 固定成本
固定成本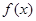 有两个零点
有两个零点 和
和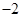 ,且
,且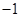 ,函数
,函数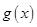 与
与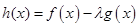 在区间
在区间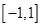 上是增函数,求实数
上是增函数,求实数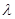 的取值范围。
的取值范围。