题目内容
f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1处取最大值,则.
- A.f(x-1)一定是奇函数
- B.f(x-1)一定是偶函数
- C.f(x+1)一定是奇函数
- D.lgx+lgy一定是偶函数
D
分析:由题意根据图象平移可以判定A、B、C是错误的,验证D即可.
解答:f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1处取最大值
图象左移一个单位,是偶函数,即f(x+1)是偶函数,所以判定A、B、C是错误的.
∵f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1处取最大值
∴lgx+lgy在x=0处取最大值,即y轴是函数lgx+lgy的对称轴
∴函数lgx+lgy是偶函数
故选D.
点评:本题考查正弦函数的奇偶性,三角函数的最值,是基础题.
分析:由题意根据图象平移可以判定A、B、C是错误的,验证D即可.
解答:f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1处取最大值
图象左移一个单位,是偶函数,即f(x+1)是偶函数,所以判定A、B、C是错误的.
∵f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1处取最大值
∴lgx+lgy在x=0处取最大值,即y轴是函数lgx+lgy的对称轴
∴函数lgx+lgy是偶函数
故选D.
点评:本题考查正弦函数的奇偶性,三角函数的最值,是基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象在y轴右侧的第一个最高点为M(2,2),与x轴在原点右侧的第一个交点为N(5,0),则函数f(x)的解析式为( )
A、2sin(
| ||||
B、2sin(
| ||||
C、2sin(
| ||||
D、2sin(
|
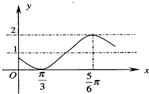 若函数f(x)=Asin(ωx+?)+B(A>0,ω>0,0<?<π)的图象如右图所示,则函数的解析式为f(x)=
若函数f(x)=Asin(ωx+?)+B(A>0,ω>0,0<?<π)的图象如右图所示,则函数的解析式为f(x)= 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象,如图
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象,如图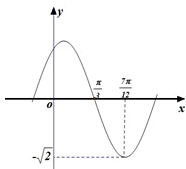 函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示.