题目内容
A={x|x2+x-6=0},B={x|mx+1=0}且A∪B=A,则m的取值范围
- A.
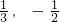
- B.
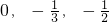
- C.
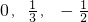
- D.
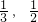
C
分析:根据已知中A={x|x2+x-6=0},B={x|mx+1=0}且A∪B=A,我们分m=0,m≠0两种情况进行讨论,分别求出满足条件的m的值,即可得到答案.
解答:∵A={x|x2+x-6=0}={-3,2},
A∪B=A,则B⊆A
若m=0,则B=∅,满足要求;
若m≠0,则B={x|x=- }
}
则m= ,或m=-
,或m=-
综上m的取值范围组成的集合为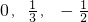
故选C
点评:本题考查的知识点是集合关系中的参数取值问题,其中本题易忽略m=0的情况,而错选A
分析:根据已知中A={x|x2+x-6=0},B={x|mx+1=0}且A∪B=A,我们分m=0,m≠0两种情况进行讨论,分别求出满足条件的m的值,即可得到答案.
解答:∵A={x|x2+x-6=0}={-3,2},
A∪B=A,则B⊆A
若m=0,则B=∅,满足要求;
若m≠0,则B={x|x=-
 }
}则m=
 ,或m=-
,或m=-
综上m的取值范围组成的集合为
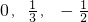
故选C
点评:本题考查的知识点是集合关系中的参数取值问题,其中本题易忽略m=0的情况,而错选A

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
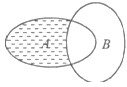 已知全集U=R,集合A={x|x2+x-2<0},B={x|0<x<3},则图中阴影部分所表示的集合为( )
已知全集U=R,集合A={x|x2+x-2<0},B={x|0<x<3},则图中阴影部分所表示的集合为( )| A、{x|-2<x≤0} | B、{x|0<x<1} | C、{x|1≤x<3} | D、{x|x≤-2或x≥3} |