题目内容
设直线y=2x-1交曲线C于A(x1,y1),B(x2,y2)两点,(1)若|x1-x2|=
| 2 |
(2)|y1-y2|=
| 2 |
分析:(1)根据题意,可得KAB=
=2,即(y1-y2)=2(x1-x2),化简可得|AB|=
=
|x1-x2|,进而可得答案,
(2)由(1)的关系,化简可得|AB|=
|x1-x2|,计算可得答案.
| y1-y2 |
| x1-x2 |
| (x1-x2)2+(y1-y2)2 |
| 5 |
(2)由(1)的关系,化简可得|AB|=
| ||
| 5 |
解答:解:(1)KAB=
=2,即(y1-y2)=2(x1-x2),
|AB|=
=
|x1-x2|=
×
=
,
(2)由(1)可得,(y1-y2)=2(x1-x2),
|AB|=
=
|x1-x2|=
×
=
.
| y1-y2 |
| x1-x2 |
|AB|=
| (x1-x2)2+(y1-y2)2 |
| 5 |
| 5 |
| 2 |
| 10 |
(2)由(1)可得,(y1-y2)=2(x1-x2),
|AB|=
| (x1-x2)2+(y1-y2)2 |
| ||
| 5 |
| 2 |
| ||
| 5 |
| ||
| 5 |
点评:本题考查两点间的距离公式的运用,注意结合直线的斜率,进行简化计算、求解.

练习册系列答案
相关题目
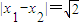 ,则|AB|= ;
,则|AB|= ;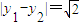 ,则|AB|= .
,则|AB|= .