题目内容
设两非零向量e1和e2不共线.(1)如果![]() =e1+e2,
=e1+e2,![]() =2e1+8e2,
=2e1+8e2,![]() =3(e1-e2),求证:A、B、D三点共线;
=3(e1-e2),求证:A、B、D三点共线;
(2)试确定实数k,使ke1+e2和e1+ke2共线.
思路分析:要证明A、B、D三点共线,需证存在λ,使![]() =λ(e1+e2)即可.而若ke1+e2和e1+ke2共线,则一定存在λ,使ke1+e2=λ(e1+ke2).
=λ(e1+e2)即可.而若ke1+e2和e1+ke2共线,则一定存在λ,使ke1+e2=λ(e1+ke2).
(1)证明:∵![]() =e1+e2,
=e1+e2,![]() =2e1+8e2+3e1-3e2=5(e1+e2)=5,
=2e1+8e2+3e1-3e2=5(e1+e2)=5,
∴![]() 、
、![]() 共线.又有公共点B,
共线.又有公共点B,
∴A、B、C三点共线.
(2)解:∵ke1+e2和e1+ke2共线,
∴存在λ,使ke1+e2=λ(e1+ke2),
则(k-λ)e1=(λk-1)e2.
由于e1与e2不共线,
只能有k-λ=0,λk-1=0.
则k=±1.
方法归纳 本题是两个向量共线的充要条件的应用,只需根据以其中某一点为起点,以另外两点为终点的向量a、b共线,存在实数λ使得a=λb(b≠0),然后利用待定系数法确定参数值.
深化升华 由平面向量共线定理可以得到以下两条常用的性质:(1)设e1、e2是两个不共线的向量,若me1+ne2=se1+te2(m、n、s、t为实数),则有![]() (2)设e1、e2是两个不共线的向量,若me1=ne2,则有m=n=0.
(2)设e1、e2是两个不共线的向量,若me1=ne2,则有m=n=0.

练习册系列答案
相关题目
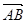 =
= +
+  ,
,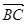 =2
=2 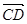 =3(
=3(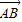 =e1+e2,
=e1+e2,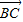 =2e1+8e2,
=2e1+8e2,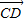 =3(e1-e2),求证:A、B、D三点共线;
=3(e1-e2),求证:A、B、D三点共线;