题目内容
设两非零向量e1和e2不共线.(1)如果![]() =e1+e2,
=e1+e2,![]() =2e1+8e2,
=2e1+8e2,![]() =3(e1,-e2),求证:A、B、D三点共线;
=3(e1,-e2),求证:A、B、D三点共线;
(2)试确定实数k,使ke1+e2和e1+ke2共线.
思路分析:本题主要考查向量基本定理和向量共线的条件.(1)可以将e1,e2看作一组基底表示我们需要的向量,如![]() ,
,![]() =
=![]() +
+![]() =2e1+8e2+3e1-3e2=5e1+5e2然后利用向量共线条件进行证明.(2)由于向量ke1+e2,e1+ke2都是用基底e1,e2表示出来的两个向量,既然两向量共线,就可以用共线条件得到(ke1+e2)=λ(e1+ke2),解出k值即可.
=2e1+8e2+3e1-3e2=5e1+5e2然后利用向量共线条件进行证明.(2)由于向量ke1+e2,e1+ke2都是用基底e1,e2表示出来的两个向量,既然两向量共线,就可以用共线条件得到(ke1+e2)=λ(e1+ke2),解出k值即可.
(1)证明:∵![]() =e1+e2,
=e1+e2,
![]() +
+![]()
=2e1+8e2+3e1-3e2
=5(e1+e2)=5![]() ,
,
∴![]() 、BD共线.又有公共点B,∴A、B、D三点共线.
、BD共线.又有公共点B,∴A、B、D三点共线.
(2)解:∵ke1+e2与e1+ke2共线,
∴存在λ使ke1+e2=λ(e1+ke2),
则(k-λ)e1=(λk-1)e2.由于e1与e2不共线,
∴只能有![]() 则k=±1.
则k=±1.
温馨提示
题目中已给出一组基底e1,e2,则该平面中任一向量都可以与之建立联系,以该基底为纽带,可以沟通不同向量之间的联系.本题要证三点共线,由这三点中任意两点确定两个向量.然后用基底e1,e2表示,并依据向量共线的条件来证明这两个向量共线.又这两个向量有公共点,于是证三点共线.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
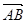 =
= +
+  ,
,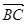 =2
=2 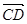 =3(
=3(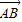 =e1+e2,
=e1+e2,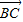 =2e1+8e2,
=2e1+8e2,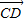 =3(e1-e2),求证:A、B、D三点共线;
=3(e1-e2),求证:A、B、D三点共线;