题目内容
设两非零向量e1和e2不共线.(1)如果
| AB |
| BC |
| CD |
(2)试确定实数k,使ke1+e2和e1+ke2共线;
(3)若|e1|=2,|e2|=3,e1与e2的夹角为60°,试确定k的值,使ke1+e2与e1+ke2垂直.
分析:(1)先证明
∥
,再根据有公共点原理,证明三点共线
(2)ke1+e2和e1+ke2共线,运用实数λ,使得ke1+e2=λ(e1+ke2),即可求出
(3)运用向量数量积公式计算:由(ke1+e2)•(e1+ke2)=0,解出K的值
| AB |
| AD |
(2)ke1+e2和e1+ke2共线,运用实数λ,使得ke1+e2=λ(e1+ke2),即可求出
(3)运用向量数量积公式计算:由(ke1+e2)•(e1+ke2)=0,解出K的值
解答:解:(1)证明:
=
+
+
=6(e1+e2)=6
,
∴
∥
,
与
有公共点A.
∴A、B、D三点共线.
(2)∵ke1+e2和e1+ke2共线,
∴存在λ使ke1+e2=λ(e1+ke2),
即(k-λ)e1+(1-λk)e2=0.
∵e1与e2为非零不共线向量,
∴k-λ=0且1-λk=0.
∴k=±1.
(3)由(ke1+e2)•(e1+ke2)=0,
k|e1|2+(k2+1)e1•e2+k|e2|2=0,得
k×22+(k2+1)×2×3×cos60°+k×32=0
?4k+3k2+3+9k=0?3k2+13k+3=0,
∴k=
.
| AD |
| AB |
| BC |
| CD |
| AB |
∴
| AB |
| AD |
| AB |
| AD |
∴A、B、D三点共线.
(2)∵ke1+e2和e1+ke2共线,
∴存在λ使ke1+e2=λ(e1+ke2),
即(k-λ)e1+(1-λk)e2=0.
∵e1与e2为非零不共线向量,
∴k-λ=0且1-λk=0.
∴k=±1.
(3)由(ke1+e2)•(e1+ke2)=0,
k|e1|2+(k2+1)e1•e2+k|e2|2=0,得
k×22+(k2+1)×2×3×cos60°+k×32=0
?4k+3k2+3+9k=0?3k2+13k+3=0,
∴k=
-13±
| ||
| 6 |
点评:此题运用平面向量基本定理考查向量共线,垂直的概念,属于综合性概念考查题

练习册系列答案
相关题目
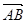 =
= +
+  ,
,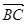 =2
=2 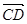 =3(
=3(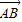 =e1+e2,
=e1+e2,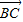 =2e1+8e2,
=2e1+8e2,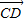 =3(e1-e2),求证:A、B、D三点共线;
=3(e1-e2),求证:A、B、D三点共线;