题目内容
若函数f（x）的导函数为f′（x）=-sinx，则函数图象在点（4，f（4））处的切线的倾斜角为（ ）
| A、90° | B、0° | C、锐角 | D、钝角 |
分析：由导函数的几何意义可知函数图象在点（4，f（4））处的切线的斜率值即为其点的导函数值，再根据k=tanα=-sin4＞0，结合正切函数的图象求出角α的范围．
解答：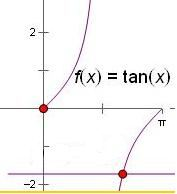
解：根据题意得f′（x）=-sinx，
则曲线y=f（x）上点（4，f（4））处的切线的斜率k=tanα=-sin4，
结合正切函数的图象
由图可得α∈（0，
），
故选C．
解：根据题意得f′（x）=-sinx，则曲线y=f（x）上点（4，f（4））处的切线的斜率k=tanα=-sin4，
结合正切函数的图象
由图可得α∈（0，
| π |
| 2 |
故选C．
点评：本题考查了导数的几何意义，以及利用正切函数的图象求倾斜角等基础知识，考查运算求解能力，考查数形结合思想．属于基础题．
练习册系列答案
相关题目
已知函数f（x）的定义域为[-3，+∞），部分函数值如表所示，其导函数的图象如图所示，若正数a，b满足f（2a+b）＜1，则
的取值范围是（ ）
| b+2 |
| a+2 |
A、(
| ||
B、(
| ||
| C、（1，4） | ||
D、(-∞，
|
已知函数f（x）的定义域为[-3，+∞），部分函数值如表所示，其导函数的图象如图所示，若正数a，b满足f（2a+b）＜1，则