题目内容
设g（x）为R上不恒等于0的奇函数，f(x)=(
+
)g(x)（a＞0且a≠1）为偶函数，则常数b的值为（ ）
| 1 |
| ax-1 |
| 1 |
| b |
| A．2 | B．1 | ||
C．
| D．与a有关的值 |
因为g（x）是奇函数，f（x）是偶函数，则根据函数奇偶性的性质可得出函数m(x)=
+
为奇函数，所以m（-x）=-m（x），即
+
=-
-
即
=-
-
=
=1，解得b=2．
故选A．
| 1 |
| ax-1 |
| 1 |
| b |
| 1 |
| a-x-1 |
| 1 |
| b |
| 1 |
| ax-1 |
| 1 |
| b |
即
| 2 |
| b |
| 1 |
| ax-1 |
| 1 |
| a-x-1 |
| ax-1 |
| ax-1 |
故选A．
练习册系列答案
相关题目
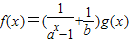（a＞0且a≠1）为偶函数，则常数b的值为______．
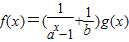（a＞0且a≠1）为偶函数，则常数b的值为（ ）