题目内容
设g(x)为R上不恒等于0的奇函数,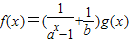 (a>0且a≠1)为偶函数,则常数b的值为______.
(a>0且a≠1)为偶函数,则常数b的值为______.
【答案】分析:根据若函数 (a>0且a≠1)为偶函数,得到f(-x)=f(x),代入函数解析式,得到恒成立的方程,整理对应相等,即可求得常数a的值.
(a>0且a≠1)为偶函数,得到f(-x)=f(x),代入函数解析式,得到恒成立的方程,整理对应相等,即可求得常数a的值.
解答:解:∵ (a>0且a≠1)为偶函数
(a>0且a≠1)为偶函数
∴ =
=
又g(x)为R上不恒等于0的奇函数,
∴g(-x)=-g(x),
即 =
=
解得b=2.
故答案为:2.
点评:考查函数的奇偶性的定义,以及方程的思想方法求参数的值,特别注意函数的定义域,属中档题.
 (a>0且a≠1)为偶函数,得到f(-x)=f(x),代入函数解析式,得到恒成立的方程,整理对应相等,即可求得常数a的值.
(a>0且a≠1)为偶函数,得到f(-x)=f(x),代入函数解析式,得到恒成立的方程,整理对应相等,即可求得常数a的值.解答:解:∵
 (a>0且a≠1)为偶函数
(a>0且a≠1)为偶函数∴
 =
=
又g(x)为R上不恒等于0的奇函数,
∴g(-x)=-g(x),
即
 =
=
解得b=2.
故答案为:2.
点评:考查函数的奇偶性的定义,以及方程的思想方法求参数的值,特别注意函数的定义域,属中档题.

练习册系列答案
相关题目
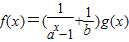 (a>0且a≠1)为偶函数,则常数b的值为( )
(a>0且a≠1)为偶函数,则常数b的值为( )