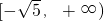题目内容
设函数 在区间[1,3]上是单调函数,则实数a的取值范围是 .
在区间[1,3]上是单调函数,则实数a的取值范围是 .
【答案】分析:先由函数,求导,再由“函数 在区间[1,3]上是单调函数”转化为“f′(x)=x2+2ax+5≥0或f′(x)=x2+2ax+5≤0在[1,3]上恒成立”,进一步转化为最值问题:a≥-(
在区间[1,3]上是单调函数”转化为“f′(x)=x2+2ax+5≥0或f′(x)=x2+2ax+5≤0在[1,3]上恒成立”,进一步转化为最值问题:a≥-( )或a≤-(
)或a≤-( )在[1,3]上恒成立,求得[-(
)在[1,3]上恒成立,求得[-( )]max,[-(
)]max,[-( )]min即可.
)]min即可.
解答:解:∵函数
∴f′(x)=x2+2ax+5
∵函数 在区间[1,3]上是单调函数
在区间[1,3]上是单调函数
∴f′(x)=x2+2ax+5≥0或f′(x)=x2+2ax+5≤0在[1,3]上恒成立
即:a≥-( )或a≤-(
)或a≤-( )在[1,3]上恒成立
)在[1,3]上恒成立
∴a≥[-( )]max或a≤[-(
)]max或a≤[-( )]min
)]min
而
∴a≥- 或a≤-3
或a≤-3
故答案为:(-∞,-3]∪
点评:本题主要考查导数法研究函数的单调性,基本思路:当函数是增函数时,导数大于等于零恒成立,当函数是减函数时,导数小于等于零恒成立,然后转化为求相应函数的最值问题.
 在区间[1,3]上是单调函数”转化为“f′(x)=x2+2ax+5≥0或f′(x)=x2+2ax+5≤0在[1,3]上恒成立”,进一步转化为最值问题:a≥-(
在区间[1,3]上是单调函数”转化为“f′(x)=x2+2ax+5≥0或f′(x)=x2+2ax+5≤0在[1,3]上恒成立”,进一步转化为最值问题:a≥-( )或a≤-(
)或a≤-( )在[1,3]上恒成立,求得[-(
)在[1,3]上恒成立,求得[-( )]max,[-(
)]max,[-( )]min即可.
)]min即可.解答:解:∵函数

∴f′(x)=x2+2ax+5
∵函数
 在区间[1,3]上是单调函数
在区间[1,3]上是单调函数∴f′(x)=x2+2ax+5≥0或f′(x)=x2+2ax+5≤0在[1,3]上恒成立
即:a≥-(
 )或a≤-(
)或a≤-( )在[1,3]上恒成立
)在[1,3]上恒成立∴a≥[-(
 )]max或a≤[-(
)]max或a≤[-( )]min
)]min而

∴a≥-
 或a≤-3
或a≤-3故答案为:(-∞,-3]∪

点评:本题主要考查导数法研究函数的单调性,基本思路:当函数是增函数时,导数大于等于零恒成立,当函数是减函数时,导数小于等于零恒成立,然后转化为求相应函数的最值问题.

练习册系列答案
相关题目
 在区间[1,3]上是单调函数,则实数a的取值范围是( )
在区间[1,3]上是单调函数,则实数a的取值范围是( ) B.
B.
 D.
D.
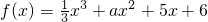 在区间[1,3]上是单调递增函数,则实数a的取值范围是
在区间[1,3]上是单调递增函数,则实数a的取值范围是