题目内容
设函数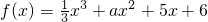 在区间[1,3]上是单调递增函数,则实数a的取值范围是
在区间[1,3]上是单调递增函数,则实数a的取值范围是
- A.(-∞,-3]
- B.

- C.
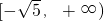
- D.(-∞,-3]∪
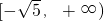
C
分析:先求出函数f(x)的导函数f′(x),根据题意,函数在区间[1,3]上是单调递增函数,即函数的导函数在区间[1,3]的值大于0,即可求出实数a的取值范围.
解答:求出函数f(x)的导函数f′(x),得f′(x)=x2+2ax+5,
根据题意可知,导函数在区间[1,3]的值大于0,
若△<0,即 时,恒成立.
时,恒成立.
若△≥0时, 或
或 ,
,
当 时,最小值为f′(a)=3a2+5恒大于0.
时,最小值为f′(a)=3a2+5恒大于0.
当 ,最小值f′(1)=6+2a≥0,得
,最小值f′(1)=6+2a≥0,得 .
.
故选C.
点评:此题主要考查函数的单调性及相关计算.
分析:先求出函数f(x)的导函数f′(x),根据题意,函数在区间[1,3]上是单调递增函数,即函数的导函数在区间[1,3]的值大于0,即可求出实数a的取值范围.
解答:求出函数f(x)的导函数f′(x),得f′(x)=x2+2ax+5,
根据题意可知,导函数在区间[1,3]的值大于0,
若△<0,即
 时,恒成立.
时,恒成立.若△≥0时,
 或
或 ,
,当
 时,最小值为f′(a)=3a2+5恒大于0.
时,最小值为f′(a)=3a2+5恒大于0.当
 ,最小值f′(1)=6+2a≥0,得
,最小值f′(1)=6+2a≥0,得 .
.故选C.
点评:此题主要考查函数的单调性及相关计算.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 在区间[1,3]上是单调函数,则实数a的取值范围是( )
在区间[1,3]上是单调函数,则实数a的取值范围是( ) B.
B.
 D.
D.
 在区间[1,3]上是单调函数,则实数a的取值范围是 .
在区间[1,3]上是单调函数,则实数a的取值范围是 .