题目内容
10. 已知x=$\frac{π}{6}$是函数f(x)=(asinx+cosx)cosx-$\frac{1}{2}$图象的一条对称轴.
已知x=$\frac{π}{6}$是函数f(x)=(asinx+cosx)cosx-$\frac{1}{2}$图象的一条对称轴.(1)求函数f(x)的单调增区间;
(2)作出函数f(x)在x∈[0,π]上的图象简图.
分析 (1)化简函数f(x),求出a的值,得出f(x)的解析式,从而求出f(x)的单调增区间;
(2)利用列表、描点、连线,画出函数f(x)在x∈[0,π]上的图象即可.
解答 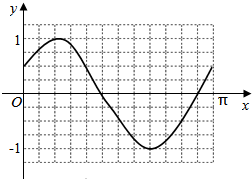 解:(1)∵f(x)=(asinx+cosx)cosx-$\frac{1}{2}$
解:(1)∵f(x)=(asinx+cosx)cosx-$\frac{1}{2}$
=asinxcosx+cos2x-$\frac{1}{2}$
=$\frac{1}{2}$asin2x+$\frac{1}{2}$cos2x,
且x=$\frac{π}{6}$是函数f(x)图象的一条对称轴,
所以f(0)=f($\frac{π}{3}$),
即$\frac{1}{2}$=$\frac{a}{2}$sin2($\frac{π}{3}$)+$\frac{1}{2}$cos2($\frac{π}{3}$),
解得a=$\sqrt{3}$,
所以f(x)=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x=sin(2x+$\frac{π}{6}$);
令-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,k∈Z,
则-$\frac{2π}{3}$+2kπ≤2x≤$\frac{π}{3}$+2kπ,k∈Z,
解得-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,k∈Z;
即函数f(x)的增区间为[-$\frac{π}{3}$+kπ,$\frac{π}{6}$+kπ],k∈Z; …(5分)
(2)列表如下,
| x | 0 | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ | π |
| 2x+$\frac{π}{6}$ | $\frac{π}{6}$ | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π | $\frac{13π}{6}$ |
| f(x) | $\frac{1}{2}$ | 1 | 0 | -1 | 0 | $\frac{1}{2}$ |
点评 本题考查了三角函数的图象与性质的应用问题,也考查了五点法画正弦函数图象的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知数列{an}中,an=11-5n,则数列{|an|}的前15项和为( )
| A. | 442 | B. | 449 | C. | 428 | D. | 421 |
18.已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am,an使得$\sqrt{{a}_{m}{a}_{n}}$=4a1,则$\frac{1}{m}$+$\frac{5}{n}$的最小值为( )
| A. | $1+\frac{{\sqrt{5}}}{3}$ | B. | $\frac{7}{4}$ | C. | 2 | D. | $\frac{11}{4}$ |
19.△ABC的内角A,B,C所对的边分别为a,b,c,且A,B,C成等差数列.命题p:“a,b,c成等比数列”;命题q:“△ABC是等边三角形”.则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.已知数列{an}中,a1=2,a2n=an+1,a2n+1=n-an,则{an}的前100项和为( )
| A. | 1250 | B. | 1276 | C. | 1289 | D. | 1300 |