题目内容
设G、M分别是△ABC的重心和外心,A(0,-a),B(0,a)(a>0),且| GM |
| AB |
(1)求点C的轨迹方程;
(2)是否存在直线m,使m过点(a,0)并且与点C的轨迹交于P、Q两点,且
| OP |
| OQ |
分析:(1)设C(x,y),则G(
,
),由题意知M(
,0),再由M为△ABC的外心,可求出点C的轨迹方程.
(2)假设直线m存在,设方程为y=k(x-a),由
得:(1+3k2)x2+6k2ax+3a2(k2-1)=0,
设P(x1,y1),Q(x2,y2),然后由根与系数的关系可以推出存在直线m,其方程为y=±
(x-a).
| X |
| 3 |
| Y |
| 3 |
| X |
| 3 |
(2)假设直线m存在,设方程为y=k(x-a),由
|
设P(x1,y1),Q(x2,y2),然后由根与系数的关系可以推出存在直线m,其方程为y=±
| 3 |
解答:解:(1)设C(x,y),则G(
,
),
因为
=λ
,所以GM∥AB,则M(
,0)
由M为△ABC的外心,则|MA|=|MC|,即
=
,
整理得:
+
=1(x≠0);(5分)
(2)假设直线m存在,设方程为y=k(x-a),
由
得:(1+3k2)x2+6k2ax+3a2(k2-1)=0,
设P(x1,y1),Q(x2,y2),则x1+x2=
,x1x2=
,
y1y2=k2(x1-a) (x2-a) =-
,
由
-
=0得:x1x2+y1y2=0,
即
+
=0,解之得k=±
,
又点(a,0)在椭圆的内部,直线m过点(a,0),
故存在直线m,其方程为y=±
(x-a).(12分)
| X |
| 3 |
| Y |
| 3 |
因为
| GM |
| AB |
| X |
| 3 |
由M为△ABC的外心,则|MA|=|MC|,即
(
|
(
|
整理得:
| x2 |
| 3a2 |
| y2 |
| a2 |
(2)假设直线m存在,设方程为y=k(x-a),
由
|
设P(x1,y1),Q(x2,y2),则x1+x2=
| 6k2a |
| 1+3k2 |
| 3a2(k2-1) |
| 1+3k2 |
y1y2=k2(x1-a) (x2-a) =-
| 2k2a2 |
| 1+3k2 |
由
| OP |
| OQ |
即
| 3a2(k2-1) |
| 1+3k2 |
| -2k2a2 |
| 1+3k2 |
| 3 |
又点(a,0)在椭圆的内部,直线m过点(a,0),
故存在直线m,其方程为y=±
| 3 |
点评:本题考查圆锥曲线知识的综合运用,解题时要注意求轨迹方程的技巧.

练习册系列答案
相关题目
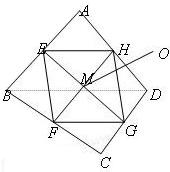 已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.
已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.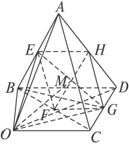
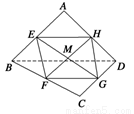
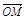 =
= (
( +
+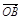 +
+ +
+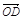 ).
).