题目内容
如图所示,已知PA是⊙O相切,A为切点,PBC为割线,弦CD//AP,AD、BC相交于E点,F为CE上一点,且

(1)求证:A、P、D、F四点共圆;
(2)若AE·ED=24,DE=EB=4,求PA的长。
【答案】
(1) 又
又 ,
,  ,
, 又
又 故
故 所以
所以 四点共圆
四点共圆
(2)
【解析】
试题分析:(1)证明: ,
,
又 ,
,  ,
, ,
,
又 故
故 ,
,
所以 四点共圆.
5分
四点共圆.
5分
(2)解:由(Ⅰ)及相交弦定理得 ,
,
又 ,
,
 ,
,
由切割线定理得 ,
,
所以 为所求. 10分
为所求. 10分
考点:平面几何知识
点评:证明四点共圆可证明四边形对角互补,求切线段长度可借助于切割线定理将其转化为割线长度

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
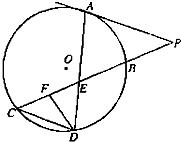 如图所示,已知PA是⊙O相切,A为切点,PBC为割线,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.
如图所示,已知PA是⊙O相切,A为切点,PBC为割线,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.

 如图所示,已知PA是⊙O相切,A为切点,PBC为割线,弦CD//AP,AD、BC相交于E点,F为CE上一点,且
如图所示,已知PA是⊙O相切,A为切点,PBC为割线,弦CD//AP,AD、BC相交于E点,F为CE上一点,且