题目内容
19.在三棱柱ABC-A′B′C′中,M,N分别为BC,B′C′的中点,化简下列式子:(1)$\overrightarrow{AM}$+$\overrightarrow{BN}$;
(2)$\overrightarrow{A′N}$-$\overrightarrow{MC′}$+$\overrightarrow{BB′}$.
分析 (1)由已知得BM$\underset{∥}{=}$NC′,从而BMC′N是平行四边形,能求出能化简$\overrightarrow{AM}$+$\overrightarrow{BN}$.
(2)结合三棱柱,利用向量加法法则能化简$\overrightarrow{A′N}$-$\overrightarrow{MC′}$+$\overrightarrow{BB′}$.
解答 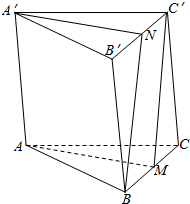 解:(1)∵在三棱柱ABC-A′B′C′中,M,N分别内BC,B′C′的中点,
解:(1)∵在三棱柱ABC-A′B′C′中,M,N分别内BC,B′C′的中点,
∴BM$\underset{∥}{=}$NC′,∴BMC′N是平行四边形,
∴$\overrightarrow{AM}$+$\overrightarrow{BN}$=$\overrightarrow{AM}+\overrightarrow{M{C}^{'}}$=$\overrightarrow{A{C}^{'}}$.
(2)$\overrightarrow{A′N}$-$\overrightarrow{MC′}$+$\overrightarrow{BB′}$
=$\overrightarrow{AM}$+$\overrightarrow{B{B}^{'}}$+$\overrightarrow{{C}^{'}M}$
=$\overrightarrow{AM}$+$\overrightarrow{C{C}^{'}}$+$\overrightarrow{{C}^{'}M}$
=$\overrightarrow{AM}$+$\overrightarrow{CM}$
=$\overrightarrow{AM}$+$\overrightarrow{MB}$
=$\overrightarrow{AB}$.
点评 本题考查向量的化简,是基础题,解题时要认真审题,注意数形结合思想的合理运用.

| A. | 2cos10° | B. | 2sin10° | C. | cos20° | D. | 1 |
| 输入 | 1 | 2 | 3 | 4 | 5 | … |
| 输出 | $\frac{1}{2}$ | $\frac{2}{5}$ | $\frac{3}{8}$ | $\frac{4}{11}$ | $\frac{5}{14}$ | … |
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
 函数f(x)=x-lnx.
函数f(x)=x-lnx. 在平行四边形ABCD中,∠CBD=90°,BC=BD=1,将平行四边形沿对角线BD折成60°的二面角(如图中实线部分).求:
在平行四边形ABCD中,∠CBD=90°,BC=BD=1,将平行四边形沿对角线BD折成60°的二面角(如图中实线部分).求: