题目内容
(本题满分13分)已知圆 的圆心在直线
的圆心在直线 上,且与
上,且与 轴交于两点
轴交于两点 ,
, .
.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)求过点
 的圆
的圆 的切线方程;
的切线方程;
(Ⅲ)已知 ,点
,点 在圆
在圆 上运动,求以
上运动,求以 ,
, 为一组邻边的平行四边形的另一个顶点
为一组邻边的平行四边形的另一个顶点 轨迹
轨迹
方程.
(Ⅰ)
(Ⅱ)
(Ⅲ) ,除去点
,除去点 和
和 .
.
【解析】
试题分析:对于第一问,注意从题的条件中去提取相关信息,找出对应的圆的圆心坐标,从而得出圆的半径,得出圆的方程,对于第二问,把握住圆与直线相切时,圆心到直线的距离等于半径,得出所求的切线方程,也可以得出点在圆上,切线和对应的半径垂直,得出切线的斜率,应用点斜式方程得出直线的方程,对于第三问,把握住平行四边形的特点,得出相应的等量关系,求出对应的结果.
试题解析:(Ⅰ) 因为圆 与
与 轴交于两点
轴交于两点 ,
, 所以圆心在直线
所以圆心在直线 上.
上.
由 得
得 即圆心
即圆心 的坐标为
的坐标为 . 2分
. 2分
半径 ,
,
所以圆 的方程为
的方程为 . 4分
. 4分
(Ⅱ)由 坐标可知点
坐标可知点 在圆
在圆 上,由
上,由
 得切线的斜率为
得切线的斜率为 ,
,
故过点
 的圆
的圆 的切线方程为
的切线方程为 . 8分
. 8分
(Ⅲ)设 , 因为
, 因为 为平行四边形,所以其对角线互相平分,
为平行四边形,所以其对角线互相平分,
即 解得
解得 1 0分
1 0分
又 在圆
在圆 上,
上,
代入圆的方程得 ,
,
即所求轨迹方程为 ,除去点
,除去点 和
和 . 13分
. 13分
考点:圆的方程,圆的切线方程,动点的轨迹方程.
考点分析: 考点1:圆系方程 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 ,则
,则 =( )
=( ) 值是( )
值是( ) 
 是单位圆上任一点,将射线OA绕点O逆时针旋转
是单位圆上任一点,将射线OA绕点O逆时针旋转 到OB交单位圆于点
到OB交单位圆于点 ,已知
,已知 若
若 的最大值为3,则
的最大值为3,则


 与椭圆
与椭圆 的中心在原点,其公共焦点
的中心在原点,其公共焦点 在
在 轴上,点
轴上,点 是
是 在第一象限的公共点.若
在第一象限的公共点.若 ,
, 的离心率是
的离心率是 ,则双曲线
,则双曲线 满足
满足 ,那么
,那么 的最大值是
的最大值是  B.
B. C.
C. D.
D.
 与圆
与圆 相交,则
相交,则 的范围为_______;
的范围为_______;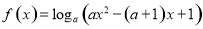
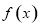 的定义域;
的定义域;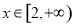 恒有
恒有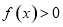 ,试确定
,试确定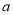 的取值范围.
的取值范围.