题目内容
(本题满分12分)已知函数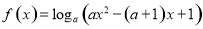
(1) 求函数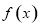 的定义域;
的定义域;
(2) 若对任意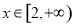 恒有
恒有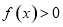 ,试确定
,试确定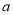 的取值范围.
的取值范围.
(1)当 时,定义域为
时,定义域为 ,当
,当 时,定义域为
时,定义域为 ;(2)
;(2) .
.
【解析】
试题分析:(1)求函数 的定义域即解
的定义域即解 的含参数
的含参数 的不等式,关键是要注意参数
的不等式,关键是要注意参数 受本身函数对数式的条件限制;(2)求解不等式
受本身函数对数式的条件限制;(2)求解不等式 在区间
在区间 恒成立,本质是转化为求函数最值问题.
恒成立,本质是转化为求函数最值问题.
试题解析:(1)由 ,即
,即 ,
,
当 时,定义域为
时,定义域为 ,
,
当 时,定义域为
时,定义域为 .
.
(2)①当 时
时 ,即
,即 ,即
,即 ,又
,又 ,
,
即 恒成立,所以
恒成立,所以 即
即 ,
,
②当 时,由
时,由 得
得 ,即
,即 ,
, ,矛盾
,矛盾
综上 .
.
考点:函数的定义域、解含参不等式、不等式恒成立、转化与化归思想、分类讨论思想.
考点分析: 考点1:对数函数 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 的圆心在直线
的圆心在直线 上,且与
上,且与 轴交于两点
轴交于两点 ,
, .
. 的方程;
的方程;
 的圆
的圆 ,点
,点 在圆
在圆 上运动,求以
上运动,求以 ,
, 为一组邻边的平行四边形的另一个顶点
为一组邻边的平行四边形的另一个顶点 轨迹
轨迹 ,
, 分别是椭圆
分别是椭圆
 的左、右焦点,过
的左、右焦点,过 与
与 轴垂直的直线交椭圆于点
轴垂直的直线交椭圆于点 ,且
,且

 ,问是否存在直线
,问是否存在直线 与椭圆交于不同的两点
与椭圆交于不同的两点 ,
, ,且
,且 的垂直平分线恰好过
的垂直平分线恰好过 点?若存在,求出直线
点?若存在,求出直线 满足约束条件
满足约束条件 ,则
,则 的最大值和最小值分别为 ( )
的最大值和最小值分别为 ( ) B.
B. C.
C. D.
D.
 的前
的前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列,若
成等差数列,若 ,则
,则 ( )
( ) 中,底面
中,底面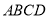 为直角梯形,
为直角梯形,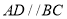 ,
,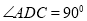 ,平面
,平面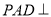 底面
底面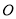 为
为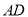 中点,
中点,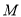 是棱PC上的点,
是棱PC上的点,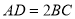 .
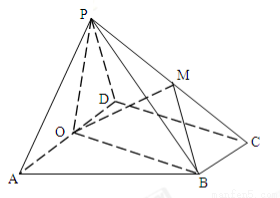
.
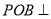 平面
平面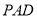 ;
;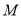 是棱
是棱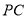 的中点,求证:
的中点,求证: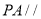 平面
平面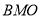 .
. 是定义在
是定义在 上的奇函数,若对于任意给定的不等实数
上的奇函数,若对于任意给定的不等实数 ,不等式
,不等式 恒成立,则不等式
恒成立,则不等式 的解集为( )
的解集为( ) B.
B. C.
C. D.
D.
 在单位正方形网格中的位置如图所示,则
在单位正方形网格中的位置如图所示,则

 :
:  ; 命题
; 命题 不等式
不等式 对
对 恒成立。如果命题
恒成立。如果命题 为真,求实数
为真,求实数 的取值范围.
的取值范围.