题目内容
【题目】在直角坐标系
中，以原点
为极点，
轴的正半轴为极轴建立极坐标系.若曲线
的极坐标方程为
，
点的极坐标为
，在平面直角坐标系中直线
经过点，且倾斜角为
.
（1）写出曲线的直角坐标方程以及点的直角坐标；
（2）设直线与曲线相交于
、
两点，求
的值.
【答案】（1）
，
；（2）
.
【解析】
（1）由
得出
，可得出
，化简变形可得出曲线
的普通方程，利用直角坐标与极坐标的转换关系可将点
的极坐标化为直角坐标；
（2）写出直线
的参数方程，设点
、
对应的参数分别为
、
，将直线的参数方程与曲线的普通方程联立，列出韦达定理，进而可得出
，求解即可.
（1）因为，，即，
两边平方整理得，所以，曲线的普通方程为.
点的直角坐标
，
，即点；
（2）直线的参数方程为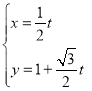
（
为参数），
将直线的参数方程与曲线的方程联立，得
，
由韦达定理得
，
，
.
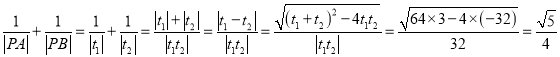阅读快车系列答案【题目】移动支付（支付宝支付，微信支付等）开创了新的支付方式，使电子货币开始普及，为了了解习惯使用移动支付方式是否与年龄有关，对某地200人进行了问卷调查，得到数据如下：60岁以上的人群中，习惯使用移动支付的人数为30人；60岁及以下的人群中，不习惯使用移动支付的人数为40人.已知在全部200人中，随机抽取一人，抽到习惯使用移动支付的人的概率为0.6.
（1）完成如下的列联表，并判断是否有
的把握认为习惯使用移动支付与年龄有关，并说明理由.
习惯使用移动支付 | 不习惯使用移动支付 | 合计（人数） | |
60岁以上 | |||
60岁及以下 | |||
合计（人数） | 200 |
（2）在习惯使用移动支付的60岁以上的人群中，每月移动支付的金额如下表：
每月支付金额 |
|
| 300以上 |
人数 | 15 |
| 5 |
现采用分层抽样的方法从中抽取6人，再从这6人中随机抽取2人，求这2人中有1人月支付金额超过3000元的概率.
附：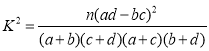
，其中
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
