题目内容
 下列两题选做一题.
下列两题选做一题.(甲)已知椭圆短轴长为2,中心与抛物线y2=4x的顶点重合,椭圆的一个焦点恰是此抛物线的焦点,求椭圆方程及其长轴的长.
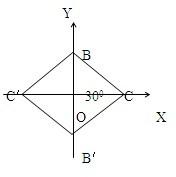
(乙)已知菱形的一对内角各为60°,边长为4,以菱形对角线所在的直线为坐标轴建立直角坐标系,以菱形60°角的两个顶点为焦点,并且过菱形的另外两个顶点作椭圆,求椭圆方程.
分析:(甲)根据椭圆的一个焦点恰是此抛物线的焦点,可求出椭圆的焦点坐标,和判断椭圆标准方程的形式,及c的值,根据a2=b2+c2,即可求得椭圆方程及其长轴的长;
(乙)由椭圆的焦点是菱形60°角的两个顶点,根据椭圆的定义可知2a=8,由图及已知条件可得b=BO=BC•sin30°=2a=BC=4,即可求出椭圆方程.
(乙)由椭圆的焦点是菱形60°角的两个顶点,根据椭圆的定义可知2a=8,由图及已知条件可得b=BO=BC•sin30°=2a=BC=4,即可求出椭圆方程.
解答:(甲)解:设所求之椭圆方程为
+
=1
∵2b=2,∴b=1.
由抛物线方程y2=4x可知它的焦点而(1,0),
所以点(1,0)也是椭圆的一个焦点,
于是c=1,从而a2=b2+c2=2,a=
,
故所求之椭圆方程为
+y2=1,长轴的长为2
.
(乙)解:设以菱形内角为600的一对顶点为端点的对角线所在的直线为X轴,
建立直角坐标系.
设椭圆方程为
+
=1.
由图及已知条件可得
b=BO=BC•sin30°=2a=BC=4.
故所求之椭圆方程为
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
∵2b=2,∴b=1.
由抛物线方程y2=4x可知它的焦点而(1,0),
所以点(1,0)也是椭圆的一个焦点,
于是c=1,从而a2=b2+c2=2,a=
| 2 |
故所求之椭圆方程为
| x2 |
| 2 |
| 2 |
(乙)解:设以菱形内角为600的一对顶点为端点的对角线所在的直线为X轴,
建立直角坐标系.
设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
由图及已知条件可得
b=BO=BC•sin30°=2a=BC=4.
故所求之椭圆方程为
| x2 |
| 16 |
| y2 |
| 4 |
点评:此题是个基础题.考查椭圆的定义和标准方程即简单的几何性质,应用了待定系数法求椭圆方程,体现了数形结合的思想方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 请考生在下列两题中任选一题作答,若两题都做,则按所做的第一题评阅计分.
请考生在下列两题中任选一题作答,若两题都做,则按所做的第一题评阅计分.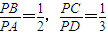 ,则
,则 的值为 .
的值为 .
