Question

【题目】某校为了探索一种新的教学模式，进行了一项课题实验，甲班为实验班，乙班为对比班，甲乙两班的人数均为50人，一年后对两班进行测试，测试成绩的分组区间为80,90、90,100、100,110、110,120、120,130，由此得到两个班测试成绩的频率分布直方图：

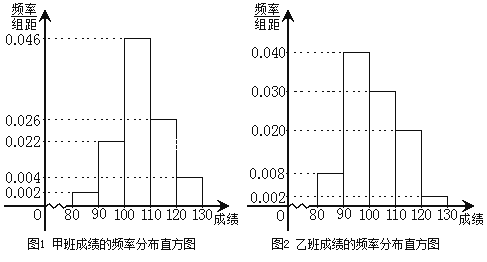
（1）完成下面2×2列联表，你能有97.5的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗？并说明理由；

	成绩小于100分	成绩不小于100分	合计
甲班			50
乙班			50
合计			100

（2）根据所给数据可估计在这次测试中，甲班的平均分是105.8，请你估计乙班的平均分，并计算两班平均分相差几分？

附：

，其中

	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	2.072	2.706	3.841	5. 024	6.635	7.879	10.828

Answer 1

【答案】（1）见解析；（2）4

【解析】分析：第一问首先应用题中的条件，结合频率分布直方图，得到相应的数据，完善列联表，之后应用公式求得观测值，之后与临界值比较大小，得到结果；第二问应用频率分布直方图中的相关数据得到对应组的人数，利用总分除以人数得到对应的平均分，进而得到两个班的平均分的差距.

详解：（1） ，，，，

，

∵，

∴有97.5的把握认为这两个班在这次测试中成绩的差异与实施课题实验有关”

（2）乙班各段人数分别是：

80,90	90,100	100,110,	110,120	120,130
4	20	15	10	1

估计乙班的平均分为：

两班平均分相差4分．