题目内容
在数列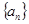 中,
中,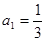 ,前
,前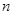 项和
项和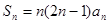 ,则数列
,则数列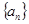 的通项公式为 ( )
的通项公式为 ( )
【答案】
A
【解析】
试题分析:由于数列 中,
中, ,前
,前 项和
项和 ,那么∵Sn=n(2n-1)an,∴当n≥2时,Sn-1=(n-1)(2n-3)an-1,,两式相减可得:an=n(2n-1)an-(n-1)(2n-3)an-1,∴(2n+1)an=(2n-3)an-1,
,那么∵Sn=n(2n-1)an,∴当n≥2时,Sn-1=(n-1)(2n-3)an-1,,两式相减可得:an=n(2n-1)an-(n-1)(2n-3)an-1,∴(2n+1)an=(2n-3)an-1, ,因此利用累积法可知数列
,因此利用累积法可知数列 的通项公式为
的通项公式为 ,选A.
,选A.
考点:数列的求和
点评:关键是根据数列的通项公式可以裂项来求和的思想得到,属于基础题。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目



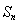















 中,其前
中,其前 项和
项和 与
与 满足关系式:
满足关系式:
 .
.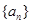 的公比为
的公比为 ,已知数列
,已知数列 ,
, ,求
,求 的值.
的值.