题目内容
在数列![]() 中,
中,![]() ,前
,前![]() 项和
项和![]() 构成公比为
构成公比为![]() 的等比数列.
的等比数列.
(Ⅰ)求证:数列![]() 不是等比数列;
不是等比数列;
(Ⅱ)设![]() ,求
,求![]()
(I)证明:由已知S1=a1=b ∵{Sn}成等比数列,且公比为q
∴Sn=bqn-1,∴Sn-1=b?qn-2(n≥2)
当n≥2时,an=Sn-Sn-1=bqn-1-bqn-2=b?(q-1)?qn-2
故当q≠1时,![]() =
=![]() =q
=q
而![]() =
=![]() =q-1≠q,∴{an}不是等比数列
=q-1≠q,∴{an}不是等比数列
当q=1,n≥2时,an=0,所以{an}也不是等比数列
综上所述,{an}不是等比数列。
(II)解:∵|q|<1,由(1)知n≥2,a2,a3,a4,…,an构成公比为q的等比数列
∴a2S2,a3S3,…,anSn是公比为q2的等比数列。
∴bn=b2+a2S2?(1+q2+q4+…+q2n-4)
∵S2=bq,a2=S2-S1=bq-b
∴a2S2=b2q(q-1)
∴bn=b2+b2q(q-1)?![]()
∵|q|<1 ∴![]() q2n-2=0
q2n-2=0
∴![]() bn=b2+b2q(q-1)?
bn=b2+b2q(q-1)?![]() =
=![]()

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目



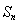















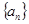 中,
中,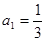 ,前
,前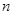 项和
项和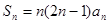 ,则数列
,则数列
 中,其前
中,其前 项和
项和 与
与 满足关系式:
满足关系式:
 .
.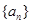 的公比为
的公比为 ,已知数列
,已知数列 ,
, ,求
,求 的值.
的值.