题目内容
对于函数y=sinxcosx的图象,下列说法正确的是( )
分析:先用二倍角公式对函数化简,然后求出函数的对称轴及对称中心,结合选项判断即可
解答:解:∵函数y=sinxcosx=
sin2x
令2x=kπ+
π可得x=
kπ+
,当k=-2可得其中一条对称轴x=-
,故A正确,B错误
令2x=kπ可得x=
kπ,C,D错误
故选:A
| 1 |
| 2 |
令2x=kπ+
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
令2x=kπ可得x=
| 1 |
| 2 |
故选:A
点评:本题考查三角函数的性质,利用二倍角公式整理,再对它的对称性(对称轴,对称中心)进行考查,从多个方面考查三角函数的性质和恒等变换.

练习册系列答案
相关题目
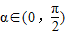 ,使
,使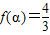 ;②存在
;②存在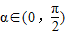 ,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点
,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点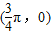 对称.
对称.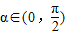 ,使
,使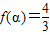 ;②存在
;②存在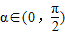 ,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点
,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点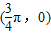 对称.
对称.