题目内容
下列对于函数y=sinx+cosx的命题中,正确命题的序号为
______.
①存在α∈(0,
),使f(α)=
;②存在α∈(0,
),使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点(
π,0)对称.
①存在α∈(0,
| π |
| 2 |
| 4 |
| 3 |
| π |
| 2 |
| 3 |
| 4 |
函数y=sinx+cosx=
sin(x+
),α∈(0,
)时 y∈(1,
],因为
∈(1,
],所以①正确.
f(x+α)=f(x+3α)说明2α是函数的周期,函数f(x)的周期为2π,显然②不正确;
③存在θ∈R使函数f(x+θ)的图象关于y轴对称,函数f(x)是周期函数,并且有对称轴,适当平移即可满足题意,所以正确.
④函数f(x)的图象关于点(
π,0)对称,当x=
时f(
)=0,满足题意,所以正确.
故答案为:①③④
| 2 |
| π |
| 4 |
| π |
| 2 |
| 2 |
| 4 |
| 3 |
| 2 |
f(x+α)=f(x+3α)说明2α是函数的周期,函数f(x)的周期为2π,显然②不正确;
③存在θ∈R使函数f(x+θ)的图象关于y轴对称,函数f(x)是周期函数,并且有对称轴,适当平移即可满足题意,所以正确.
④函数f(x)的图象关于点(
| 3 |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
故答案为:①③④

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
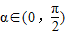 ,使
,使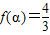 ;②存在
;②存在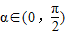 ,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点
,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点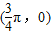 对称.
对称.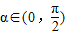 ,使
,使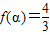 ;②存在
;②存在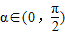 ,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点
,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点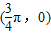 对称.
对称.