题目内容
(本题满分14分)
如图,在多面体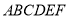 中,四边形
中,四边形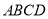 是菱形,
是菱形,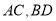 相交于点
相交于点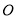 ,
,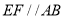 ,
,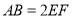 ,平面
,平面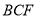
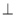 平面
平面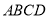 ,
,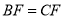 ,点
,点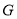 为
为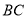 的中点.
的中点.

(1)求证:直线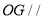 平面
平面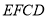 ;
;
(2)求证:直线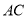
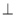 平面
平面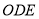 .
.
(1)详见解析(2)详见解析
【解析】
试题分析:(1)∵四边形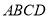 是菱形,∴点
是菱形,∴点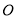 是
是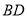 的中点,∵点
的中点,∵点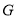 为
为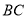 的中点,由三角形中位线性质得
的中点,由三角形中位线性质得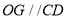 ,再根据线面平行判定定理得直线
,再根据线面平行判定定理得直线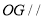 平面
平面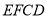 .
.
(2)一方面∵四边形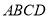 是菱形,∴
是菱形,∴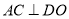 ,另一方面∵
,另一方面∵ 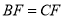 ,点
,点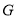 为
为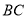 的中点, ∴
的中点, ∴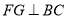 ,由面面垂直性质定理得
,由面面垂直性质定理得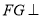 平面
平面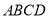 ,从而
,从而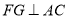 ,又可证四边形
,又可证四边形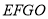 为平行四边形,即
为平行四边形,即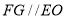 ,所以
,所以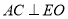 ,最后由线面垂直判定定理得
,最后由线面垂直判定定理得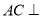 平面
平面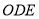 .
.
试题解析:证明(1)∵四边形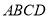 是菱形,
是菱形,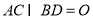 ,∴点
,∴点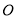 是
是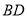 的中点,
的中点,
∵点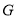 为
为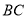 的中点 ∴
的中点 ∴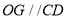 , 3分
, 3分
又∵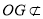 平面
平面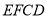 ,
,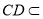 平面
平面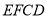 ,∴直线
,∴直线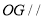 平面
平面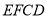 . 7分
. 7分
(2)∵ 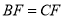 ,点
,点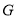 为
为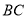 的中点, ∴
的中点, ∴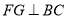 ,
,
∵平面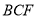
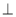 平面
平面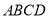 ,平面
,平面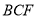
 平面
平面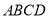
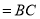 ,
,
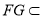 平面
平面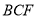 ,
,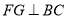 ∴
∴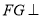 平面
平面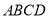 , 9分
, 9分
∵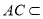 平面
平面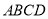 ∴
∴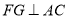 ,
,
∵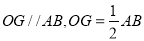 ,
,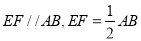 ,∴
,∴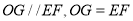 ,
,
∴四边形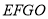 为平行四边形, ∴
为平行四边形, ∴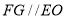 , 11分
, 11分
∵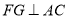 ,
,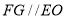 ,∴
,∴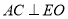 , ∵四边形
, ∵四边形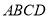 是菱形,∴
是菱形,∴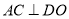 ,
,
∵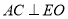 ,
,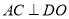 ,
,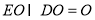 ,
,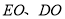 在平面
在平面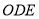 内,
内,
∴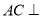 平面
平面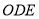 . 14分
. 14分
考点:线面平行判定定理,线面垂直判定定理,面面垂直性质定理
考点分析: 考点1:点、线、面之间的位置关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 的展开式中含有
的展开式中含有 项,则n的最小值为 【 】
项,则n的最小值为 【 】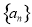 ,
,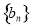 ,
,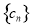 满足:
满足: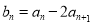 ,
,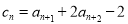 ,
,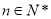 .
. 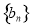 是等差数列;
是等差数列;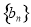 ,
,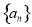 从第二项起为等差数列;
从第二项起为等差数列;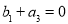 时,数列
时,数列 的最小正周期为 .
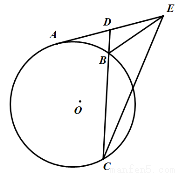
的最小正周期为 .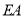 与圆
与圆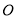 相切于点
相切于点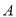 ,
,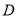 是
是 的割线,与圆
的割线,与圆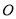 相交于点
相交于点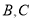 ,连结
,连结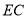 .
.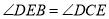 .
.
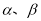 是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号) 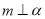 ,则在平面
,则在平面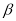 内,一定不存在与直线
内,一定不存在与直线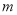 平行的直线.
平行的直线.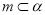 ,则在平面
,则在平面 的定义域为 .
的定义域为 . 的焦点为顶点,顶点为中心,离心率为2的双曲线标准方程为 .
的焦点为顶点,顶点为中心,离心率为2的双曲线标准方程为 .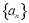 的公比为
的公比为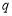 (
(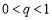 ),前n项和为
),前n项和为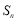 ,若
,若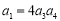 ,且
,且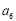 与
与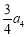 的等差中项为
的等差中项为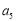 ,则
,则 .
.