题目内容
数列![]() 的各项均为正值,
的各项均为正值,![]() ,对任意
,对任意![]() ,
,![]() ,
,![]() 都成立.
都成立.
求数列![]() 、
、![]() 的通项公式;
的通项公式;
当![]() 且
且![]() 时,证明对任意
时,证明对任意![]() 都有
都有![]() 成立.
成立.
(1) ![]()
![]() (2)同解析
(2)同解析
解析:
解:由![]() 得,
得,
![]()
数列![]() 的各项为正值,
的各项为正值,![]()
∴![]()
∴![]()
又![]()
∴数列![]() 为等比数列.
为等比数列.
∴![]() ,
, ![]() ,即为数列
,即为数列![]() 的通项公式.
的通项公式.
![]()
(2)设![]()
∴![]() (1)
(1)
当![]() 时,
时,![]() ,
,![]()
∴![]()
∴![]() , 当且仅当
, 当且仅当![]() 时等号成立.
时等号成立.
上述(1)式中,![]() ,
,![]() ,
,![]() 全为正,所以
全为正,所以
![]()
∴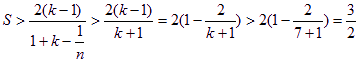 得证.
得证.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
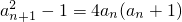 ,bn=log2(an+1)都成立.
,bn=log2(an+1)都成立.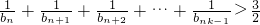 成立.
成立.