题目内容
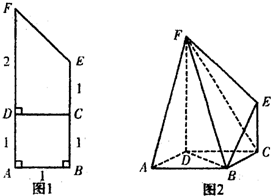 (2013•许昌二模)将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连结部分线段后围成一个空间几何体,如图2所示.
(2013•许昌二模)将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连结部分线段后围成一个空间几何体,如图2所示.(Ⅰ)求证:BE∥面ADF;
(Ⅱ)求二面角D-BF-E的大小.
分析:(I)取DF的中点M,连结AM、EM,可证出EM∥AB且EM=AB,从而得到四边形ABEM是平行四边形,得AM∥BE.根据线面平行的判定定理,可证出BE∥平面ADF;
(II)分别以以DA、DC、DF所在直线为x轴、y轴、z轴,建立空间直角坐标系D-xyz,如图所示.得到A、B、C、E、F各点的坐标,从而得到
、
和
的坐标,利用垂直的两个向量数量积为零列式,解出
=(1,1,1)是平面BEF的一个法向量,而
=
=(-1,1,0)是平面BDF的一个法向量,用公式算出
、
的夹角为90°,从而得到平面BDF与平面BEF互相垂直,即得二面角D-BF-E的大小为90°.
(II)分别以以DA、DC、DF所在直线为x轴、y轴、z轴,建立空间直角坐标系D-xyz,如图所示.得到A、B、C、E、F各点的坐标,从而得到
| AC |
| BE |
| BF |
| n |
| m |
| AC |
| m |
| n |
解答:解:(I)取DF的中点M,连结AM、EM,则DM=EC=1且DM∥EC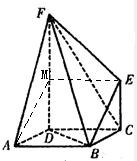
∴四边形CDME是平行四边形,可得EM∥CD且EM=CD
又∵AB∥CD且AB=CD,得EM∥AB且EM=AB
∴四边形ABEM是平行四边形,可得AM∥BE
∵AM?平面ADF,BE?平面ADF,∴BE∥平面ADF;
(II)连结AC
∵平面ABCD⊥平面DCEF,ABCD为正方形,DCEF为直角梯形,
∴以DA所在直线为x轴、DC所在直线为y轴、DF所在直线为z轴,
建立空间直角坐标系D-xyz,如图所示
可得A(1,0,0),B(1,1,0),C(0,0,1),E(0,1,1),F(0,0,2)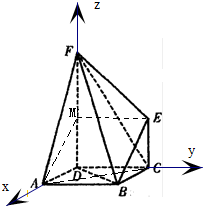
∵AC⊥BD,AC⊥DF,BD、DF是平面BDF内的相交直线
∴AC⊥平面BDF,可得
=
=(-1,1,0)是平面BDF的一个法向量
设平面BEF的一个法向量为
=(x,y,z),
由
,取z=1得x=y=1,可得
=(1,1,1)
∵cos<
,
>=
=
=0
∴
⊥
,即平面BDF的法向量与平面BEF的法向量互相垂直
因此,平面BDF与平面BEF互相垂直,可得二面角D-BF-E的大小为90°.

∴四边形CDME是平行四边形,可得EM∥CD且EM=CD
又∵AB∥CD且AB=CD,得EM∥AB且EM=AB
∴四边形ABEM是平行四边形,可得AM∥BE
∵AM?平面ADF,BE?平面ADF,∴BE∥平面ADF;
(II)连结AC
∵平面ABCD⊥平面DCEF,ABCD为正方形,DCEF为直角梯形,
∴以DA所在直线为x轴、DC所在直线为y轴、DF所在直线为z轴,
建立空间直角坐标系D-xyz,如图所示
可得A(1,0,0),B(1,1,0),C(0,0,1),E(0,1,1),F(0,0,2)

∵AC⊥BD,AC⊥DF,BD、DF是平面BDF内的相交直线
∴AC⊥平面BDF,可得
| m |
| AC |
设平面BEF的一个法向量为
| n |
由
|
| n |
∵cos<
| m |
| n |
|
| ||||
|
| -1×1+1×1+0×1 | ||||
|
∴
| m |
| n |
因此,平面BDF与平面BEF互相垂直,可得二面角D-BF-E的大小为90°.
点评:本题以折叠问题为载体,在四棱锥中证明线面平行,并求二面角的大小.着重考查了空间直线与平面平行的判定定理、直线与平面垂直的判定定理和利用空间向量研究平面与平面所成角等知识,属于中档题.

练习册系列答案
相关题目
 (2013•许昌二模)如图,已知PE切圆O于点E,割线PBA交圆O于A,B两点,∠APE的平分线和AE、BE分别交于点C,D
(2013•许昌二模)如图,已知PE切圆O于点E,割线PBA交圆O于A,B两点,∠APE的平分线和AE、BE分别交于点C,D