题目内容
若函数f(x)= 为奇函数,则a的取值范围为________.
为奇函数,则a的取值范围为________.
(0,1]
分析:f(x)= 中,a>0,由
中,a>0,由 在定义域内是一个偶函数,x∈
在定义域内是一个偶函数,x∈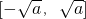 ,知g(x)=|x+1|-1 为奇函数,由此能求出a的取值范围.
,知g(x)=|x+1|-1 为奇函数,由此能求出a的取值范围.
解答:∵f(x)= 中,x≠0,a-x2≥0,
中,x≠0,a-x2≥0,
∴a≥x2>0,
∵ 在定义域内是一个偶函数,x∈
在定义域内是一个偶函数,x∈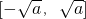 ,
,
∴要函数f(x)= 为奇函数,则g(x)=|x+1|-1 为奇函数,
为奇函数,则g(x)=|x+1|-1 为奇函数,
(1)当-1≤x≤1时,g(x)=x+1-1=x;
(2)当x>1时,g(x)=x+1-1=x;
(3)当x<-1时,g(x)=-x-1-1=-x-2
所以只有定义域为[-1,1]的子区间,且定义域关于0对称时,g(x)才是奇函数
所以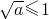 ,即a≤1,
,即a≤1,
所以0<a≤1.
故答案为:(0,1].
点评:本题考查函数的奇偶性的应用,解题时要认真审题,仔细解答,注意分类讨论思想的灵活运用.
分析:f(x)=
 中,a>0,由
中,a>0,由 在定义域内是一个偶函数,x∈
在定义域内是一个偶函数,x∈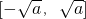 ,知g(x)=|x+1|-1 为奇函数,由此能求出a的取值范围.
,知g(x)=|x+1|-1 为奇函数,由此能求出a的取值范围.解答:∵f(x)=
 中,x≠0,a-x2≥0,
中,x≠0,a-x2≥0,∴a≥x2>0,
∵
 在定义域内是一个偶函数,x∈
在定义域内是一个偶函数,x∈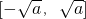 ,
,∴要函数f(x)=
 为奇函数,则g(x)=|x+1|-1 为奇函数,
为奇函数,则g(x)=|x+1|-1 为奇函数,(1)当-1≤x≤1时,g(x)=x+1-1=x;
(2)当x>1时,g(x)=x+1-1=x;
(3)当x<-1时,g(x)=-x-1-1=-x-2
所以只有定义域为[-1,1]的子区间,且定义域关于0对称时,g(x)才是奇函数
所以
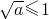 ,即a≤1,
,即a≤1,所以0<a≤1.
故答案为:(0,1].
点评:本题考查函数的奇偶性的应用,解题时要认真审题,仔细解答,注意分类讨论思想的灵活运用.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目