题目内容
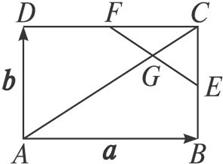
如图2-2-3，已知ABCD为平行四边形，过点A和B的圆与AD、BC分别交于E、F.求证：C、D、E、F四点共圆.
图2-2-3
思路分析：连结EF.由∠B+∠AEF=180°，∠B+∠C=180°，可得∠AEF=∠C.
证明：连结EF.∵ABCD为平行四边形，∴∠B+∠C=180°.
∵A、B、F、E内接于圆，∴∠B+∠AEF=180°.
∴∠AEF=∠C.∴C、D、E、F四点共圆.
深化升华 要证明四点共圆，首先要把这四个点连结组成四边形，然后说明其对角互补或外角等于它的内对角.
练习册系列答案
教材全解字词句篇系列答案
相关题目
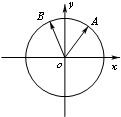如图，在平面直角坐标系中，锐角α和钝角β的终边分别与单位圆交于A，B两点．
=a，
=b，用a、b表示
=_____________.
