题目内容
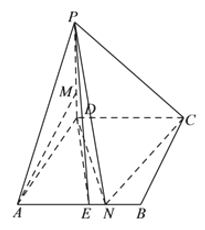
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中点.
中点.
(I)求证:直线![]() 平面
平面![]() .
.
(II)求证:直线![]() 平面
平面![]() .
.
(III)在![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,若存在,确定
,若存在,确定![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
【答案】(I)见解析;(Ⅱ)见解析(III)![]() 与
与![]() 重合.点
重合.点![]() 的位置为所求.
的位置为所求.
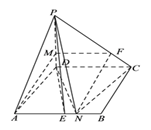
【解析】试题分析:(I)结合条件中给出的线段间的长度关系,在![]() 上取点
上取点![]() ,使
,使![]() ,证明四边形
,证明四边形![]() 为平行四边形,可得
为平行四边形,可得![]() ,故可得结论;(II)结合图形分析可得只需证
,故可得结论;(II)结合图形分析可得只需证![]() ,
, ![]() ,便可得到
,便可得到![]() 平面
平面![]() ;(III)建立空间直角坐标系,用向量法通过计算进行判断可得结果。
;(III)建立空间直角坐标系,用向量法通过计算进行判断可得结果。
试题解析:
证明:(I)在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
, ![]() ,
,
因为![]() ,
, ![]() ,
,
所以![]() ,且
,且![]() ,
,
因为![]() ,
, ![]() ,
,
所以![]() ,且
,且![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,
又![]() 平面
平面![]() ,
, ![]()
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
(Ⅱ)因为![]() 是
是![]() 中点,底面
中点,底面![]() 是菱形,
是菱形, ![]() ,
,
所以![]() ,
,
因为![]() ,
,
所以![]() ,
,
所以![]() .
.
又![]() 平面
平面![]() ,
,
所以![]()
又 ![]()
所以直线![]() 平面
平面![]()
(III)由(Ⅱ)可知![]() ,
, ![]() ,
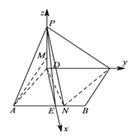
, ![]() ,相互垂直,以
,相互垂直,以![]() 为原点,建立如图所示的空间直角坐标系D-xyz.
为原点,建立如图所示的空间直角坐标系D-xyz.
则![]() ,
,  ,
, 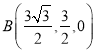 ,
,
假设存在点G满足条件,其坐标为
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由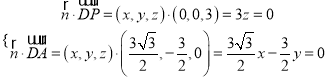 ,得
,得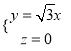 ,
,
令![]() ,则
,则![]()
同理可得平面![]() 的法向量
的法向量![]() ,
,
由题意得
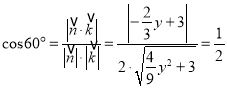 ,
,
解得![]()
所以点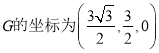 。
。
所以当点![]() 与点
与点![]() 重合时,二面角
重合时,二面角![]() 的大小为
的大小为![]() .
.
因此点![]() 为所求的点。
为所求的点。

【题目】某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
顾客数(人) | x | 30 | 25 | y | 10 |
结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知这100位顾客中一次购物量超过8件的顾客占55%.
(Ⅰ)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(Ⅱ)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率.
(注:将频率视为概率)