题目内容
如图1,在四棱锥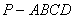 中,
中,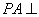 底面
底面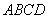 ,面
,面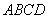 为正方形,
为正方形,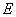 为侧棱
为侧棱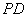 上一点,
上一点,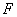 为
为 上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.
上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.
(Ⅰ)求四面体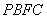 的体积;
的体积;
(Ⅱ)证明: ∥平面
∥平面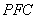 ;
;
(Ⅲ)证明:平面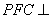 平面
平面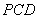 .
.
 |
(Ⅰ)解:由左视图可得 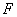 为
为 的中点,
的中点,
 所以 △
所以 △ 的面积为
的面积为  .
.
因为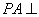 平面
平面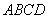 , …
, …
所以四面体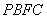 的体积为
的体积为

 .
.
(Ⅱ)证明:取 中点
中点 ,连结
,连结 ,
, .
.
由正(主)视图可得 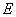 为
为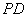 的中点,所以
的中点,所以 ∥
∥ ,
, .
.
又因为 ∥
∥ ,
, , 所以
, 所以 ∥
∥ ,
, .
.
所以四边形 为平行四边形,所以
为平行四边形,所以 ∥
∥ .
.
因为  平面
平面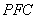 ,
, 平面
平面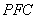 ,
,
所以 直线 ∥平面
∥平面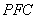 .
.
(Ⅲ)证明:因为 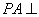 平面
平面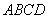 ,所以
,所以  .
.
因为面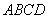 为正方形,所以
为正方形,所以  .
.
所以  平面
平面 .
.
因为  平面
平面 ,所以
,所以  .
.
因为  ,
,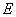 为
为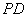 中点,所以
中点,所以  .
.
所以  平面
平面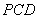 .
.
因为  ∥
∥ ,所以
,所以 平面
平面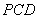 .
.
因为  平面
平面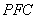 , 所以 平面
, 所以 平面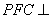 平面
平面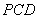 .
.

练习册系列答案
相关题目
 -1,0,1},B={x|1≤
-1,0,1},B={x|1≤ <4},则A∩B等于
<4},则A∩B等于 的棱长为
的棱长为 ,动点P在对角线
,动点P在对角线 上,过点P作垂直于
上,过点P作垂直于 ,记这样得到的截面多边形
,记这样得到的截面多边形 x,
x, 则当
则当 时,函数
时,函数 的值域为( )
的值域为( )



 ” 之值,
” 之值,




 ,
, 随机取自集合
随机取自集合 ,则直线
,则直线 与圆
与圆 有公共点的概率是
有公共点的概率是 在以点
在以点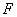 为焦点的抛物线
为焦点的抛物线 上,则
上,则
 B.
B. C.
C. D.
D.
 学生中阅读时间在
学生中阅读时间在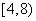 小时内的人数为_____.
小时内的人数为_____.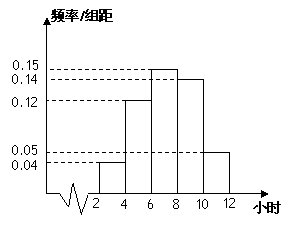
 为互不重合的三条直线,平面
为互不重合的三条直线,平面 平面
平面 ,
, ,
, ,那么
,那么 是
是 的
的 的右焦点与抛物线
的右焦点与抛物线 的焦点重合,则
的焦点重合,则 .
.