题目内容
在区间[0，10]中任意取一个数，则它与4之和大于10的概率是 ．
考点：几何概型
专题：概率与统计
分析：所取之数与4之和大于10可得6＜x≤10，长度与10之比即为所求概率．
解答：
解：在区间[0，10]中任意取一个数x，
则它与4之和大于10的x满足x+4＞10，
解得6＜x≤10，
∴所求概率为
=
；
故答案为：
．
则它与4之和大于10的x满足x+4＞10，
解得6＜x≤10，
∴所求概率为
| 10-6 |
| 10 |
| 2 |
| 5 |
故答案为：
| 2 |
| 5 |
点评：本题考查几何概型；如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．属基础题．
练习册系列答案
相关题目
若抛物线y2=2px（p＞0）上一点Q到准线和抛物线的对称轴的距离分别为10和6，则此点Q的横坐标为（ ）
| A、1 | B、9 | C、2 | D、1或9 |
已知抛物线C：y2=2px（p＞0）的准线为l，焦点为F，圆M的圆心在x轴的正半轴上，圆M与y轴相切，过原点O作倾斜角为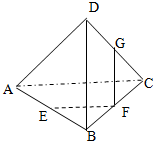
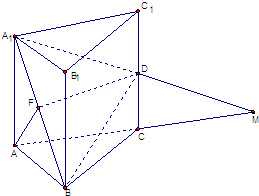已知正三棱柱A1B1C1-ABC中，AA1=AB=a，D是CC1的中点，F是A1B的中点，A1D与AC的延长线交于点M（如图），
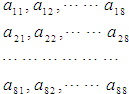64个正数排成8行8列，如图所示：在符号aij（1≤i≤8，1≤j≤8）中，i表示该数所在的行数，j表示该数所在的列数．已知每一行中的数依次都成等差数列，而每一列中的数依次都成等比数列（每列公比q都相等）且a11=解下列不等式：
（1）|4x-3|＜21；
（2）|
+2|≥
；
（3）
＞
；
（4）|x+3|＞x+3；
（5）|3x-4|＞2x-1；
（6）|3x-4|≤x-1．
（1）|4x-3|＜21；
（2）|
| x-1 |
| 2 |
| 3 |
| 4 |
（3）
| |3x-1|-1 |
| 2 |
| |1-3x|+1 |
| 3 |
（4）|x+3|＞x+3；
（5）|3x-4|＞2x-1；
（6）|3x-4|≤x-1．
在四边形ABCD中，若
=
+
，则四边形ABCD的形状一定是（ ）
| AC |
| AB |
| AD |
| A、平行四边形 | B、菱形 |
| C、矩形 | D、正方形 |
已知
，则
的最大值为（ ）
|
| y-2 |
| x-3 |
| A、2 | ||
B、
| ||
| C、0 | ||
D、
|