题目内容
设AB是圆x2+y2=1的一条直径,以AB为直角边、B为直角顶点,逆时针方向作等腰直角三角形ABC.当AB变动时,求C点的轨迹.
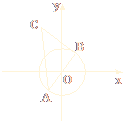
所求轨迹是以原点为圆心,![]() 为半径的圆.
为半径的圆.
解析:
解法一:(参数法)取∠xOB=θ为参数,则B(cosθ,sinθ),
于是,(x-cosθ)2+(y-sinθ)2=4.
![]() =-cotθ,消去θ得x2+y2=5.
=-cotθ,消去θ得x2+y2=5.
故所求轨迹是以原点为圆心,![]() 为半径的圆.
为半径的圆.
解法二:(相关点法)设C(x,y)、B(x0,y0),
当x0、y0≠0时,
则(x-x0)2+(y-y0)2=4.
![]() ·
·![]() =-1.由x02+y02=1消去x0、y0得轨迹方程.显然当x0=0或y0=0时,方程也适合.
=-1.由x02+y02=1消去x0、y0得轨迹方程.显然当x0=0或y0=0时,方程也适合.
解法三:(几何法)连结CO,因为|OC|2=|OB|2+|AB|2=5为定值,故其轨迹为圆.
评析:求轨迹的方法很多,注意合理选取,参数法求轨迹方程是常用方法之一,常用到的参数有斜率、点的坐标、长度、夹角等.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
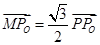 .
.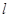 :y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.
:y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.