题目内容
设点P是圆x2 +y2 =4上任意一点，由点P向x轴作垂线PP0，垂足为Po，且
．
（Ⅰ）求点M的轨迹C的方程；
（Ⅱ）设直线
：y=kx+m(m≠0)与（Ⅰ）中的轨迹C交于不同的两点A，B．
（1）若直线OA，AB，OB的斜率成等比数列，求实数m的取值范围；
（2）若以AB为直径的圆过曲线C与x轴正半轴的交点Q，求证：直线过定点(Q点除外)，并求出该定点的坐标．
解：（Ⅰ）设点
，
，则由题意知
.
由
，
，且
，
得
.
所以
于是
又
，所以
.
所以，点M的轨迹C的方程为
.………………………………（3分）
（Ⅱ）设
，
.
联立
得
.
所以，
，即
. ①
且
（i）依题意，
，即
.
.
，即
.
，
，解得
.
将代入①，得
.
所以，
的取值范围是
.
）曲线与
轴正半轴的交点为
.
依题意，
， 即
.
于是
.
，
即
，
.
化简，得
.
解得，
或
，且均满足.
当时，直线的方程为
，直线过定点
(舍去)；
当时，直线的方程为
，直线过定点
.
所以，直线过定点.
练习册系列答案
阅读快车系列答案
相关题目
．
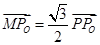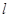：y=kx+m(m≠0)与（Ⅰ）中的轨迹C交于不同的两点A，B．
=
．
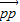