题目内容
2.已知椭圆C1的中心为原点O,离心率e=$\frac{\sqrt{2}}{2}$,其中一个焦点的坐标为(-$\sqrt{2}$,0)(Ⅰ)求椭圆C1的标准方程;
(Ⅱ)当点Q(u,v)在椭圆C1上运动时,设动点P(2v-u,u+v)的运动轨迹为C2,若点T满足:$\overrightarrow{OT}$=$\overrightarrow{MN}$+2$\overrightarrow{OM}$+$\overrightarrow{ON}$,其中M,N是C2上的点,直线OM,ON的斜率之积为-$\frac{1}{2}$,试说明:是否存在两个定点F1,F2,使得|TF1|+|TF2|为定值?若存在,求F1,F2的坐标;若不存在,说明理由.
分析 (Ⅰ)由椭圆离心率e=$\frac{\sqrt{2}}{2}$,其中一个焦点的坐标为(-$\sqrt{2}$,0),列出方程组,求出a,b,由此能求出椭圆方程.
(Ⅱ)设M(x1,y1),N(x2,y2),P(x,y),T(m,n),推导出m=x1+2x2,n=y1+2y2,设kOM,kON分别为直线OM,ON的斜率,由已知条件得x1x2+2y1y2=0,利用点差法能求出存在两定点F1,F2,且为椭圆$\frac{{x}^{2}}{60}+\frac{{y}^{2}}{30}$=1的两个焦点,使得|TF1|+|TF2|为定值,并能求出其坐标.
解答 解:(Ⅰ)∵椭圆C1的中心为原点O,离心率e=$\frac{\sqrt{2}}{2}$,其中一个焦点的坐标为(-$\sqrt{2}$,0),
∴$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{c=\sqrt{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=$\sqrt{2}$,
∴椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$.
(Ⅱ)设M(x1,y1),N(x2,y2),P(x,y),T(m,n),
则$\left\{\begin{array}{l}{x=2v-μ}\\{y=μ+v}\end{array}\right.$,∴$\left\{\begin{array}{l}{μ=\frac{1}{3}(2y-x)}\\{v=\frac{1}{3}(x+y)}\end{array}\right.$,
∵点Q(μ,v)在椭圆C1上运动,
∴$\frac{{μ}^{2}}{4}+\frac{{v}^{2}}{2}$=1,
[$\frac{1}{3}$(2y-x)]2+2[$\frac{1}{3}$(x+y)]2=4,
x2+2y2=12,
∴动点P的轨迹方程为x2+2y2=12,
由$\overrightarrow{OT}=\overrightarrow{MN}+2\overrightarrow{OM}+\overrightarrow{ON}$,得:
(m,n)=(x2-x1,y2-y1)+2(x1,y1)+(x2,y2)=(x1+2x2,y1+2y2),
∴m=x1+2x2,n=y1+2y2,
设kOM,kON分别为直线OM,ON的斜率,由已知条件得${k}_{OM}•{k}_{ON}=\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$,
∴x1x2+2y1y2=0,
∵点M,N在椭圆C2上,
∴${{x}_{1}}^{2}+2{{y}_{1}}^{2}$=12,${{x}_{2}}^{2}+2{{y}_{2}}^{2}$=12,
∴m2+2n2=(${{x}_{1}}^{2}+4{{x}_{2}}^{2}+4{x}_{1}{x}_{2}$)+2(${{y}_{1}}^{2}+4{{y}_{2}}^{2}+4{y}_{1}{y}_{2}$)
=(${{x}_{1}}^{2}+2{{y}_{1}}^{2}$)+4(${{x}_{2}}^{2}+2{{y}_{2}}^{2}$)+4(x1x2+2y1y2)=60,
∴T点是椭圆$\frac{{x}^{2}}{60}+\frac{{y}^{2}}{30}=1$上的点,
∴存在两定点F1,F2,且为椭圆$\frac{{x}^{2}}{60}+\frac{{y}^{2}}{30}$=1的两个焦点,
使得|TF1|+|TF2|为定值,
其坐标分别为(-$\sqrt{30}$,0),($\sqrt{30}$,0).
点评 本题考查椭圆方程的求法,考查满足条件的点是否存在的判断与求法,考查推理论证能力、运算求解能力,考查转化化归思想,是中档题.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 如图在正方体ABCD-A1B1C1D1中,P是上底面A1B1C1D1内一动点,PM垂直AD于M,PM=PB,则点P的轨迹为( )
如图在正方体ABCD-A1B1C1D1中,P是上底面A1B1C1D1内一动点,PM垂直AD于M,PM=PB,则点P的轨迹为( )| A. | 线段 | B. | 椭圆一部分 | C. | 抛物线一部分 | D. | 双曲线一部分 |
| A. | 1 | B. | 5 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
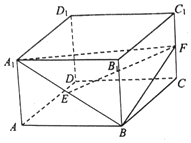 如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.
如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.