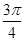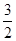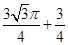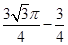题目内容
可导函数 的导函数为
的导函数为 ,且满足:①
,且满足:① ;②
;② ,记
,记 ,
,  ,
, 则
则 的大小顺序为( )
的大小顺序为( )
A. | B. | C. | D. |
C
解析试题分析:因为 是减函数,则根据复合函数可知
是减函数,则根据复合函数可知 是增函数,构造函数
是增函数,构造函数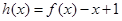 ,则
,则 ,因为
,因为 ,所以当
,所以当 时
时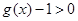 ,所以
,所以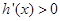 ,所以
,所以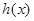 在
在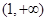 上单调递增,所以
上单调递增,所以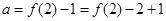 ,
,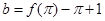 ,
,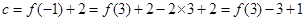 ,而
,而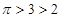 ,所以
,所以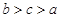 ,故选C.
,故选C.
考点:1.利用导数研究函数的单调性;2.复合函数的单调性.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
(原创)若对定义在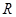 上的可导函数
上的可导函数 ,恒有
,恒有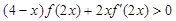 ,(其中
,(其中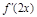 表示函数
表示函数 的导函数
的导函数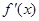 在
在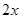 的值),则
的值),则 ( )
( )
| A.恒大于等于0 | B.恒小于0 |
| C.恒大于0 | D.和0的大小关系不确定 |
把函数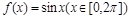 的图像向左平移
的图像向左平移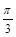 后,得到
后,得到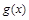 的图像,则
的图像,则 与
与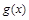 的图像所围成的图形的面积为( )
的图像所围成的图形的面积为( )
| A.4 | B.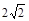 | C.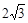 | D.2 |
用边长为48厘米的正方形铁皮做一个无盖的铁盒时,在铁皮的四角各截去一个面积相等的小正方形,然后把四边折起,就能焊成铁盒.当所做的铁盒的容积最大时,在四角截去的正方形的边长为( )
| A.12 | B.10 | C.8 | D.6 |
若存在x使不等式 >
>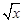 成立,则实数m的取值范围为( )
成立,则实数m的取值范围为( )
A.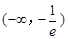 | B. | C. | D. |
等比数列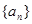 的前n项和为Sn,若
的前n项和为Sn,若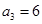 ,
,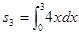 ,则公比q的值为( )
,则公比q的值为( )
| A.1 | B.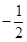 | C.l或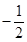 | D.-1或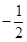 |
函数f(x)=ln(x+1)- 的零点所在的大致区间是( )
的零点所在的大致区间是( )
| A.(0,1) | B.(1,2) |
| C.(2,e) | D.(3,4) |
设函数f(x)=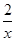 +ln x,则( ).
+ln x,则( ).
A.x=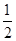 为f(x)的极大值点 为f(x)的极大值点 |
B.x=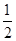 为f(x)的极小值点 为f(x)的极小值点 |
| C.x=2为f(x)的极大值点 |
| D.x=2为f(x)的极小值点 |
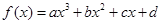 在
在 ,
, 点处取到极值,其中
点处取到极值,其中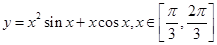 上,则曲线
上,则曲线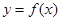 的切线的斜率的最大值是( )
的切线的斜率的最大值是( )