Question

已知函数f（x）满足f（1+x）+f（1-x）=2，且直线y=k（x-1）+1与f（x）的图象有5个交点，则这些交点的纵坐标之和为（　　）

A．10

B．5

C．4

D．3

Answer 1

分析：由题意可得函数f（x）关于点（1，1）中心对称，这5个交点在直线直线y=k（x-1）+1上，点（1，1）必是交点之一．设5个交点的纵坐标分别为 y₁，y₂，y₃，y₄，y₅，其中有 y₃=1，可知y₁与y₅、y₂与y₄ 均关于直线y=1对称，由此求得这些交点的纵坐标之和．

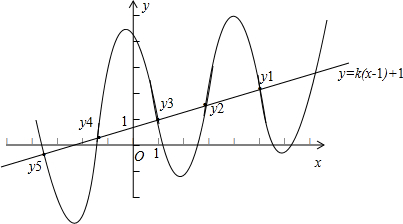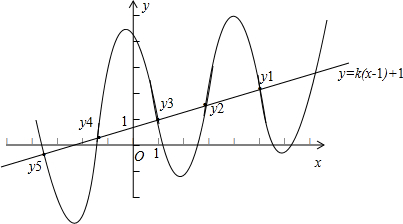解答：解：对于任何函数y=f（x）：若满足f（x+a）+f（b-x）=c，则此函数关于点（

a+b

2

，

c

2

）对称．
∴函数f（x）关于点（1，1）中心对称．
∵直线y=k（x-1）+1与f（x）的图象5有个交点，且对称点是成对的，∴点（1，1）必是交点之一．
由题意可知这5个交点在直线直线y=k（x-1）+1上．
设5个交点的纵坐标分别为 y₁，y₂，y₃，y₄，y₅，其中有 y₃=1． 可知y₁与y₅、y₂与y₄ 均关于y=1对称．
y₅=1-（ y₁-1）；y₄=1-（ y₂-1），
∴y₁+y₂+y₃+y₄+y₅=5，
∴这些交点的纵坐标之和为5，
故选B．

点评：本题主要考查函数的零点与方程的根的关系，体现了转化的数学思想，属于中档题．