题目内容
给定抛物线C:y2=4x,F是C的焦点,过点F的直线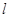 与C相交于A、B两点。
与C相交于A、B两点。
(1)设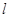 的斜率为1,求
的斜率为1,求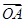 与
与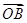 夹角的余弦值;
夹角的余弦值;
(2)设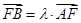 ,若
,若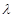 ∈[4,9],求
∈[4,9],求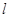 在y轴上截距的变化范围。
在y轴上截距的变化范围。
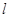 与C相交于A、B两点。
与C相交于A、B两点。(1)设
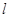 的斜率为1,求
的斜率为1,求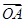 与
与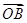 夹角的余弦值;
夹角的余弦值;(2)设
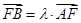 ,若
,若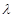 ∈[4,9],求
∈[4,9],求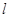 在y轴上截距的变化范围。
在y轴上截距的变化范围。解:(1)
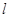 的方程为
的方程为 、设
、设 ,
,
由


 ,
,
 。。。。。。。。。。。。6分
。。。。。。。。。。。。6分(2)
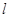 的方程为
的方程为 、设
、设 ,
,
由
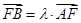

由


 ,由
,由

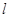 在y轴上截距的变化范围:
在y轴上截距的变化范围: 。。。。。。。。。。12分
。。。。。。。。。。12分略

练习册系列答案
相关题目
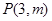 在以点
在以点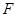 为焦点的抛物线
为焦点的抛物线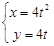 (
(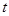 为参数)上,则
为参数)上,则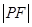 等于( )
等于( ) 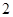
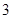
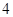
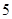
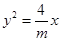 的焦点与椭圆
的焦点与椭圆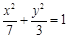 的左焦点重合,则
的左焦点重合,则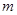 的值为( )
的值为( )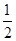
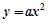 的准线方程是
的准线方程是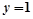 ,则
,则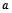 的值为( )
的值为( )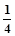
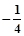
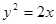 内一点A(1,1)作弦BC,若A为BC的中点,则直线BC的方程为
内一点A(1,1)作弦BC,若A为BC的中点,则直线BC的方程为 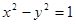 的中心,焦点是双曲线的右顶点.
的中心,焦点是双曲线的右顶点.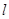 过点
过点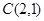 交抛物线于
交抛物线于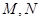 两点,是否存在直线
两点,是否存在直线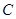 恰为弦
恰为弦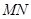 的中点?若存在,求出直线
的中点?若存在,求出直线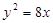 ,双曲线的右焦点是抛物线的焦点,离心率为2,则双曲线的标准方程是 .
,双曲线的右焦点是抛物线的焦点,离心率为2,则双曲线的标准方程是 .  的准线方程为
的准线方程为 ,则
,则 的值为
的值为



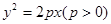 的焦点为
的焦点为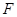 ,过点
,过点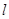 与抛物线交于
与抛物线交于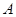 、
、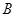 两点,抛物线的准线与
两点,抛物线的准线与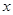 轴交于点
轴交于点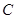 .
.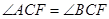 ;
;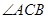 的最大值,并求
的最大值,并求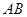 的长.
的长.