题目内容
若对所有正数x,y,不等式 都成立,则a的最小值是
都成立,则a的最小值是
- A.

- B.2
- C.

- D.8
A
分析:不等式 ?
? ≤a,只需用不等式求
≤a,只需用不等式求 的最大值即可.
的最大值即可.
解答:x,y为正数,由x2+y2≥2xy,
得2(x2+y2)≥(x+y)2,所以 ≥x+y.
≥x+y.
 ?
? ≤a,
≤a,
又 ≤
≤ =
= ,
,
所以a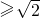 ,即a的最小值为
,即a的最小值为 .
.
故选A.
点评:本题考查函数恒成立及应用不等式求最值,函数恒成立问题往往转化为函数的最值问题处理.
分析:不等式
 ?
? ≤a,只需用不等式求
≤a,只需用不等式求 的最大值即可.
的最大值即可.解答:x,y为正数,由x2+y2≥2xy,
得2(x2+y2)≥(x+y)2,所以
 ≥x+y.
≥x+y. ?
? ≤a,
≤a,又
 ≤
≤ =
= ,
,所以a
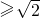 ,即a的最小值为
,即a的最小值为 .
.故选A.
点评:本题考查函数恒成立及应用不等式求最值,函数恒成立问题往往转化为函数的最值问题处理.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 都成立,则a的最大值是( )
都成立,则a的最大值是( )
 都成立,则a的最大值是( )
都成立,则a的最大值是( )