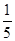题目内容
若矩阵
满足下列条件：①每行中的四个数所构成的集合均为
；②四列中至少有两列的上下两数是相同的．则这样的不同矩阵的个数为（ ）
| A．48 | B．72 | C．168 | D．312 |
C
解析试题分析：若恰有两列的上下两数相同，取这两列有
种，从1，2，3，4中取2个数排这两列，有
种，排另外两列有
种，所以共有
种；若恰有三列的上下两数相同，也是恰有四列上下两数相同，有
种(只要排其中一行即可). 故一共有
种.
考点：1.分析问题解决问题的能力；2.排列组合问题.
练习册系列答案
相关题目
已知
的最小值是
，则二项式
展开式中
项的系数为（ ）
A． | B． | C． | D． |
我们把个位数字之和为6的四位数称为“六合数”（如2013是“六合数”），则“六合数”中首位为2的“六合数”共有（ ）
| A．18个 | B．15个 | C．12个 | D．9个 |
将一个四棱锥的每个顶点染上一种颜色，并使同一条棱上的两个端点异色，若只有5种颜色可供使用,则不同的染色方法总数有 （ ）
| A． 240种 | B． 300种 | C．360种 | D．420种 |
若
＝
＋
＋
＋…＋
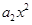（x∈R），则
＋
＋
+…+
( )
A．－ | B． | C．－ | D． |
设m∈N*，且m＜45，则(45-m)(46-m)(47-m)……(60-m)，用排列数符号表示为( )
| A．A60-m15 | B．A60-m16 | C．A60-m45-m | D．A45-m16 |
从
,六个数字中任取两个奇数和两个偶数，组成没有重复数字的四位奇数，有多少种取法
A． | B． | C． | D． |