题目内容
将一个四棱锥的每个顶点染上一种颜色,并使同一条棱上的两个端点异色,若只有5种颜色可供使用,则不同的染色方法总数有 ( )
| A. 240种 | B. 300种 | C.360种 | D.420种 |
D
解析试题分析:四棱锥为 .下面分两种情况即
.下面分两种情况即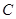 与
与 同色与
同色与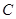 与
与 不同色来讨论,(1)各个点的不同的染色方法
不同色来讨论,(1)各个点的不同的染色方法
 ,
, :
: ,
, :
: ,
,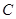 与
与 同色:1,
同色:1, :
: ,故共有
,故共有  种.(2)各个点的不同的染色方法
种.(2)各个点的不同的染色方法 
 ,
, :
: ,
, :
: ,
,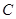 与
与 不同色
不同色 ,
, :
: ,故共有
,故共有 种,由分步计数原理可得不同的染色方法总数有
种,由分步计数原理可得不同的染色方法总数有  . 故选
. 故选 .
.
考点:分步计数原理.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
某学校周五安排有语文、数学、英语、物理、化学、体育六节课,要求体育不排在第一节课,数学不排在第四节课,则这天课表的不同排法种数为( )
| A.600 | B.288 | C.480 | D.504 |
(1-x)3(1- )3展开式中常数项是( )
)3展开式中常数项是( )
| A.-20 | B.18 | C.20 | D.0 |
若矩阵 满足下列条件:①每行中的四个数所构成的集合均为
满足下列条件:①每行中的四个数所构成的集合均为 ;②四列中至少有两列的上下两数是相同的.则这样的不同矩阵的个数为( )
;②四列中至少有两列的上下两数是相同的.则这样的不同矩阵的个数为( )
| A.48 | B.72 | C.168 | D.312 |
用1,2,3三个数字组成一个四位数字,规定这三个数必须同时使用,且同一数字不能相邻出现,这样的四位数共有
| A.18个 | B.9个 | C.12个 | D.24个 |
某餐厅有 四个桌子,每个桌子最多坐8人,现有11人进入餐厅,随意的坐下吃饭,已知
四个桌子,每个桌子最多坐8人,现有11人进入餐厅,随意的坐下吃饭,已知 桌一定有人坐,其他桌子可能有人坐,也可能没人坐,则四个桌子坐的人数的不同的情况有多少种( )
桌一定有人坐,其他桌子可能有人坐,也可能没人坐,则四个桌子坐的人数的不同的情况有多少种( )
| A.286 | B.276 | C.264 | D.246 |
二项式 的展开式的第二项的系数为
的展开式的第二项的系数为 ,则
,则 的值为( )
的值为( )
A. | B. | C. 或 或 | D. 或 或 |
 的展开式中所有项重新排成一列,有理式不相邻的排法有( )种.
的展开式中所有项重新排成一列,有理式不相邻的排法有( )种.



 名志愿者中选出
名志愿者中选出 名,分别从事
名,分别从事 ,
, ,
, ,
, 四项不同的工作,每人承担一项.若甲、乙二人均不能从事
四项不同的工作,每人承担一项.若甲、乙二人均不能从事 种
种 
 种
种  种
种