题目内容
在平面直角坐标系中,不等式
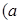 为常数
为常数 表示的平面区域的面积为8,则
表示的平面区域的面积为8,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
B
解析试题分析:根据题意,由于平面直角坐标系中,不等式
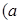 为常数
为常数 表示的平面区域的面积为8,那么结合图像可知S=
表示的平面区域的面积为8,那么结合图像可知S= ,那么所求解的目标函数
,那么所求解的目标函数 可变形为
可变形为 ,表示的为区域内点到(-3,1)的斜率的范围加上1的范围即可,结合条件可知(
,表示的为区域内点到(-3,1)的斜率的范围加上1的范围即可,结合条件可知( )与(-3,1)的连线的斜率为最小值
)与(-3,1)的连线的斜率为最小值 ,选B.
,选B.
考点:线性规划的运用。
点评:解决该试题的关键是利用不等式组表示的平面区域,然后结合面积得到参数a的值,进而求解区域内殿到定点的斜率的几何意义,中档题。

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
已知 满足
满足 ,则
,则 的最小值为( )
的最小值为( )
| A.6 | B.8 | C.12 | D.15 |
不等式组 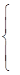
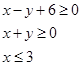 ,表示平面区域的面积为( )
,表示平面区域的面积为( )
| A.12 | B.18 | C. 32 | D.36 |
若整数x,y满足不等式组  则2x+y的最大值是
则2x+y的最大值是
| A.11 | B.23 | C.26 | D.30 |
若实数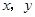 满足
满足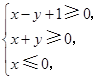 则
则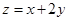 的最小值是( )
的最小值是( )
| A.0 | B.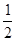 | C.1 | D.2 |
已知变量x,y满足约束条件 ,则z=3|x|+y的取值范围为( )
,则z=3|x|+y的取值范围为( )
| A.[-1,5] | B.[1, 11] | C.[5, 11] | D.[-7, 11] |
已知平面区域如右图所示, 在平面区域内取得最大值的最优解有无数多个,则
在平面区域内取得最大值的最优解有无数多个,则 的值为 ( )
的值为 ( )
A. | B. | C. | D.不存在 |
如果实数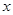 、
、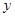 满足条件
满足条件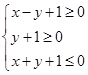 ,那么
,那么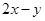 的最大值为( )
的最大值为( )
A.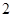 | B.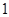 | C.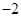 | D.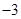 |
 的取值范围是
的取值范围是


