题目内容
已知函数f(x)满足f(a+b)=f(a)•f(b)(其中a,b∈R),f(1)=3,则 =________.
=________.
6
分析:先利用赋值法求出f2(2)与f(4)的关系,再将条件转化一下求出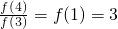 ,从而求出所求.
,从而求出所求.
解答:∵函数f(x)满足f(a+b)=f(a)•f(b)(其中a,b∈R),
∴f(2+2)=f(4)=f(2)f(2)=f2(2)
f(1+3)=f(4)=f(1)f(3)?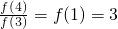
∴ =
=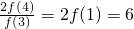
故答案为6.
点评:本题主要考查了抽象函数及其应用,以及赋值法的应用,属于基础题.
分析:先利用赋值法求出f2(2)与f(4)的关系,再将条件转化一下求出
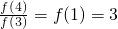 ,从而求出所求.
,从而求出所求.解答:∵函数f(x)满足f(a+b)=f(a)•f(b)(其中a,b∈R),
∴f(2+2)=f(4)=f(2)f(2)=f2(2)
f(1+3)=f(4)=f(1)f(3)?
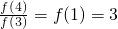
∴
 =
=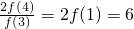
故答案为6.
点评:本题主要考查了抽象函数及其应用,以及赋值法的应用,属于基础题.

练习册系列答案
相关题目