题目内容
(本题满分12分)在直角坐标系xOy中，直线l的参数方程为：
(t为参数)，若以O为极点，x轴正半轴为极轴建立极坐标系，则曲线C的极坐标方程为r=
cos(θ+
)，求直线l被曲线C所截的弦长．
【答案】
【解析】
试题分析：将方程
(t为参数)化为普通方程得，3x+4y+1=0，………3分
将方程r=
cos(θ+
)化为普通方程得，x2+y2-x+y=0， ……………6分
它表示圆心为(
，-)，半径为
的圆， …………………………9分
则圆心到直线的距离d=
， ……………………………10分
弦长为2
． ……………………12分
考点：直线参数方程，圆的极坐标方程及直线与圆的位置关系
点评：先将参数方程极坐标方程转化为普通方程
练习册系列答案
相关题目
．
，求△ABC的面积．
，0），若实数λ使向量
，λ
，
满足λ2·（
时，过点A1且斜率为1的直线与此时（1）中的曲线相交的另一点为B，能否在直线x=-9上找一点C，使ΔA1BC为正三角形（请说明理由）。
中
分别为A,B,C所对的边，
且
，求
的取值范围
中，数列的前n项和
满足
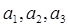；（2） 由（1）猜想数列
中，E是BC的中点，F是
的中点
的平面角的余弦值。