题目内容
在无穷数列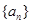 中,
中,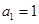 ,对于任意
,对于任意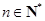 ,都有
,都有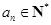 ,
,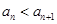 . 设
. 设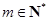 , 记使得
, 记使得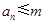 成立的
成立的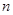 的最大值为
的最大值为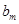 .
.
(1)设数列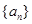 为1,3,5,7,
为1,3,5,7,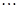 ,写出
,写出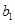 ,
,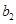 ,
,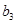 的值;
的值;
(2)若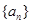 为等比数列,且
为等比数列,且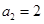 ,求
,求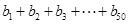 的值;
的值;
(3)若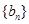 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列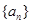 .
.
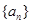 中,
中,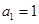 ,对于任意
,对于任意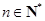 ,都有
,都有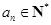 ,
,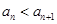 . 设
. 设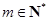 , 记使得
, 记使得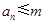 成立的
成立的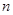 的最大值为
的最大值为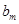 .
.(1)设数列
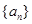 为1,3,5,7,
为1,3,5,7,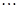 ,写出
,写出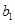 ,
,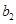 ,
,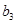 的值;
的值;(2)若
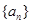 为等比数列,且
为等比数列,且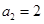 ,求
,求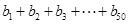 的值;
的值;(3)若
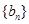 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列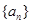 .
.(1)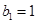 ,
,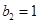 ,
,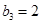 ;(2)
;(2) ;(3)得
;(3)得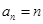
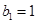 ,
,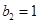 ,
,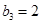 ;(2)
;(2) ;(3)得
;(3)得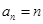
试题分析:(1)根据使得
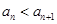 成立的
成立的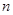 的最大值为
的最大值为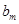 ,
,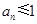 ,则
,则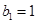 ,
,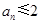 ,则
,则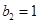 ,
,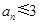 ,则
,则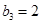 ,这样就写出
,这样就写出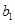 ,
,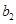 ,
,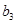 的值;(2)确定
的值;(2)确定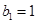 ,
,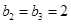 ,
,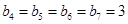 ,
, ,
,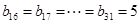 ,
,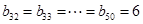 ,分组求和,即可求
,分组求和,即可求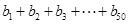 的值;(3)若
的值;(3)若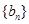 为等差数列,先判断
为等差数列,先判断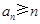 ,再证明
,再证明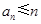 ,即可求出所有可能的数列
,即可求出所有可能的数列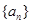 .
.(1)
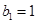 ,
,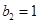 ,
,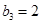 . 3分
. 3分(2)因为
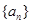 为等比数列,
为等比数列,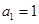 ,
,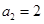 ,
,所以
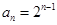 , 4分
, 4分因为使得
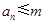 成立的
成立的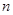 的最大值为
的最大值为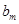 ,
,所以
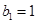 ,
,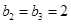 ,
,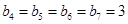 ,
, ,
,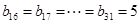 ,
,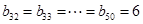 , 6分
, 6分所以
 . 8分
. 8分(3)由题意,得
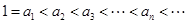 ,
,结合条件
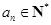 ,得
,得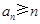 . 9分
. 9分又因为使得
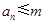 成立的
成立的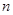 的最大值为
的最大值为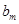 ,使得
,使得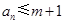 成立的
成立的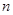 的最大值为
的最大值为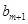 ,
,所以
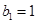 ,
,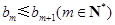 . 10分
. 10分设
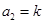 ,则
,则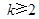 .
.假设
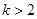 ,即
,即 ,
,则当
 时,
时,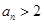 ;当
;当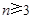 时,
时,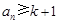 .
.所以
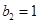 ,
,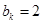 .
.因为
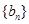 为等差数列,
为等差数列,所以公差
 ,
,所以
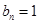 ,其中
,其中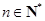 .
.这与
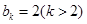 矛盾,
矛盾,所以
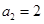 . 11分
. 11分又因为
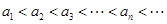 ,
,所以
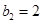 ,
,由
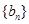 为等差数列,得
为等差数列,得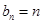 ,其中
,其中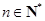 . 12分
. 12分因为使得
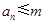 成立的
成立的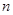 的最大值为
的最大值为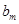 ,
,所以
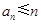 ,
,由
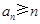 ,得
,得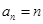 . 13分
. 13分
练习册系列答案
相关题目
 通项为
通项为 ,则
,则 .
. 同时满足:(1)各项均不为
同时满足:(1)各项均不为 ,(2)存在常数k, 对任意
,(2)存在常数k, 对任意 都成立,则称这样的数列
都成立,则称这样的数列 是否为“类等比数列”?说明理由.
是否为“类等比数列”?说明理由. (a,b为常数),是否存在常数λ,使得
(a,b为常数),是否存在常数λ,使得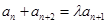 对任意
对任意 都成立?若存在,求出λ;若不存在,请举出反例.
都成立?若存在,求出λ;若不存在,请举出反例. (a,b为常数),求数列
(a,b为常数),求数列 的前n项之和
的前n项之和 ;数列
;数列 的前n项之和记为
的前n项之和记为 ,求
,求 .
. 的前n项和为
的前n项和为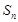 ,
, ,且对任意的
,且对任意的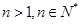 均满足
均满足 .
. ,
, ,
, (
( ),求数列
),求数列 的前
的前 项和
项和 .
. +f(x),x∈R,且f(1)=
+f(x),x∈R,且f(1)= ,则数列{f(n)}(n∈N*)的前20项的和为( )
,则数列{f(n)}(n∈N*)的前20项的和为( ) x+an+1cos x-an+2sin x满足f′
x+an+1cos x-an+2sin x满足f′ =0.
=0. ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn. 是4和16的等差中项,则
是4和16的等差中项,则